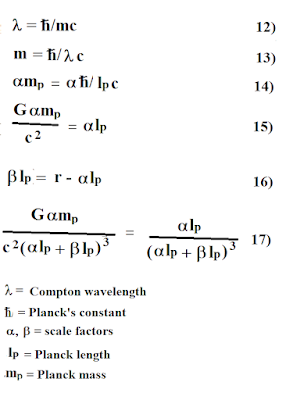ABSTRACT:
According to Relativity Theory, everything propagates through spacetime at light speed. However, a mass at rest propagates solely through time and experiences zero velocity. A massless photon propagates solely through space and experiences no time. Other objects propagate through time and space, and, experience both time and subluminal velocities. This paper demonstrates that both gravity (the fundamental interaction) and gravitational waves propagate at light speed through spacetime, but with varying degrees through time and space, i.e., they each have different velocities through space.
The year was 1971. Via the Apollo 15 mission, David Scott performed the following experiment on the moon: With a hammer in one hand and a feather in the other, he held them the same distance from the moon's surface. He dropped them. They hit the ground simultaneously. This experiment might not seem like a big deal, but it confirms that Galileo was correct. More importantly, it shows that gravitational interactions (with the exception of gravitational waves) should never be modeled after the electromagnetic (EM) force.
The EM force, like Newtonian forces, conserves energy, momentum and itself in the following manner:
Equations 1 and 2 above show that different masses have different velocities and different rates of acceleration when acted on by the same magnitude of force. Since momentum is conserved, we can use equations 2 above and 3 below to predict the speed of the photons that mediate the force:
No surprises here. Photons propagate at c as expected. Gravity, unlike EM, is full of surprises. Let's model gravity after the EM force and see what happens. Let's assume there is a gravitational field of gravitons that mediate the "force" of gravity. Here is the math:
At 6 and 7 above, force and momentum are not conserved. If we assume momentum is conserved, at 8 the speed of gravitons depends on the mass of the falling object. We cannot count on their speed being c. What about gravitational waves? Why do they consistently propagate at or near the speed of light? Consider the following thought experiment:
You throw a baseball with enough force to place it into orbit around the earth. The force you use is independent of and counters gravity. It is also conserved and so is the ball's angular momentum. The ball's tangential velocity depends on its mass and vice versa. As the ball orbits earth its velocity changes, i.e., the ball accelerates. An accelerating mass emits gravitational waves (GWs). The energy converted to GWs is the same conserved energy you put into the ball when you threw it into orbit. We can predict the speed of these GWs the same way we predicted the speeds of photons and gravitons:
From an airplane flying 10,000 feet above the earth's surface, drop several items with different masses. If we assume they are falling to earth, they all fall at the same rate, so momentum at any instant is not conserved. But what if those items are at rest and it is the earth with mass M falling or accelerating to the items? Clearly, an independent force accelerating the earth would be conserved. With more mass, the earth would accelerate less. The problem is, with more mass the earth really accelerates more. This fact implies that there is no independent force causing earth to accelerate. So there is apparently no independent force acting on the earth or the items that appear to be falling.
If the earth simply accelerates to the items, what need is there for a graviton? As shown at 6 through 8 above, gravitons, if they exist, fail to either conserve force, energy and momentum, or, they don't have a consistent speed if force, energy and momentum are conserved. David Scott's experiment showed us this is true. The feather and the hammer fell at the same rate, not different rates.
Laplace and Van Flandern, based on observations, concluded that the speed of gravity must be several orders of magnitude faster than light. Perhaps infinite! (Masses simply accelerating towards one another combined with independant forces causing angular momentum could certainly provide that impression.) Other physicists hate the idea of infinite speed and insist the speed of gravity is c. To accommodate the Laplace and Van Flandern observations, they point to a model of moving charges, where one charge's vector is lined up with the another charge's instant position rather than its retarded position, creating the illusion that there is no light-time delay, i.e., infinite photon speed when in reality photon speed is c. This model is then projected onto a cosmological scale, and thus moving planets and stars work in a similar fashion and create the illusion of infinite graviton speed when in reality graviton speed is allegedly c. The problem with this model is it completely ignores the Heisenberg Uncertainty Principle. For the model to work, one has to know the position and velocity of the charges with precision. And, as demonstrated above, charges (or EM) conserve force and momentum in a way that gravity does not.
Laplace, Van Flandern and the physicists who criticize them have one thing in common: they all think of gravity as a force consisting of bosons that either propagate at c or much faster than c. Because of General Relativity, it makes perfect sense that most physicists want to limit the speed of gravity to c; however, when two black holes collide and form a new more massive singularity, it is not clear how a boson propagating at c can escape that singularity and inform the rest of the universe of the event. Since nothing propagating at c can escape a black hole, how does this new black hole singularity reset the curvature of its surrounding spacetime?
Let's start with what we know. At 12 below we have the Compton wavelength equation. Note that when mass m changes, the wavelength must change instantaneously, since a mass and its wavelength are essentially the same entity. If we think of the wavelength as spacetime, then spacetime is updated the instant mass changes. At 14 we convert the equation to Planck units with an alpha scale factor. At 15 we derive a Scharzschild radius. Equation 16 shows that a change in alpha instantaneously causes a change in beta, since their sum times a Planck length make up distance r. (Distance r, of course, along with the mass, determines the rate of Newtonian acceleration.) Equation 17 is a scalar version of Einstein's field equations. On the right side we have curvature units.
When two black holes merge, alpha increases everywhere it appears at equation 17. This causes an instantaneous decrease of beta at any distance r from the new black hole's singularity. Thus the new black hole doesn't have to send information at light speed or any speed to update its surrounding spacetime. Mass and spacetime have an entangled relationship. Energy and momentum equations show this to be true. Where would energy and momentum be without mass entangled with velocity? Of course velocity is in units of space and time. Thus one can conclude that the only valid speed for gravity is how fast matter moves at an arbitrary distance from a falling observer:
Equation 18 above shows how fast gravity moves through space. Equation 19 shows how fast gravity moves through time. Finally, equation 20 shows how fast gravity moves through spacetime--the speed of light.
References:
1. Ibison, Michael, Puthoff, Harold E., Little, Scott. The Speed of Gravity Revisited.
2. Kopeikin, Sergei, Fomalont, Edward B. 27 Mar 2006. Aberration and the Fundamental Speed of Gravity in the Jovian Deflection Experiment.
3. Flanagan, Eanna. Hughes, Scott A. 2005. The Basics of Gravitational Wave Theory. New Journal of Physics.
4. Carlip, S. Aberration and the Speed of Gravity. December 1999.
5. Van Flandern, T. 1999. The Speed of Gravity What the Experiments Say. Meta Research University of Maryland Physics Army Research Lab.
6. Siegel, Ethan. August 30, 2018. Our Motion Through Space Isn't A Vortex, But Something Far More Interesting. Forbes
7. Galileo's Leaning Tower of Pisa experiment. Wikipedia.
8. David Scott does the feather hammer experiment on the moon | Science News. Youtube.com
9. Tzortzakakis, Filippos, LIGO Analysis: Direct Detection of Gravitational Waves. Journal of Research Progress Vol. 1.
