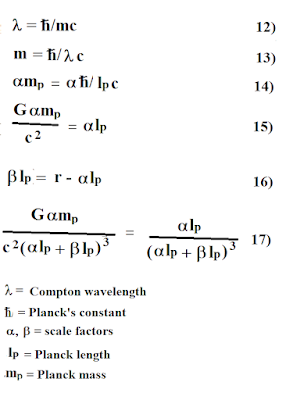ABSTRACT:
This paper shows why entanglement is not limited to the quantum realm, and shows how entanglement and superluminal speed is not only possible, but consistent with special and general relativity.
Imagine two photons. Photon A and photon B are propagating in opposite directions. According to the velocity addition formula, their combined velocity v is as follows:
Now, imagine two observers, Alice and Bob. Alice looks at each photon individually and notices that they each propagate at c. Bob looks at both photons at once and notes that their combined velocity is c. At this point, you probably have some questions: How does photon A seem to know that photon B is propagating in the opposite direction? It's not like photon B can send a signal to photon A (a signal that would have to be faster than light) to let photon A know that it needs to cut its velocity in half along with photon B so their combined velocity will be no faster than light. Further, how do A and B seem to know that Bob is watching them both? They also seem to know that Alice is watching only one of them. The one she's watching seems to adjust its velocity to c just for her benefit. It's as if the photons are entangled with each other and also entangled with all observers.
Einstein described quantum entanglement as "spooky action at a distance"--yet, where would the velocity addition formula be without "spooky action at a distance"? Below is a mathematical derivation of the entanglement of two particles with velocities v1 and v2:
Equation 7 above shows that, at any distance r (the distance between the two particles), any change of velocities (v1, v2) must lead to an instantaneous change in velocity v; otherwise, light speed c would not be constant in a vacuum. Note that the terms on the right side are in units of frequency and wavelength. To maintain a constant light speed requires any change of frequency to be instantly offset by a change of wavelength. Additionally, this entangled relationship between frequency and wavelength is shown by equation 9 below:
At 11 above is a scalar version of Einstein's field equations. Equation 10 shows that velocity v can be infinite if distance r drops to zero. How is this possible given that infinite energy is required to accelerate mass m to light speed? Equation 9 provides the answer: the infinite velocity is achieved with just the rest-mass energy (E). No force acts on mass m. If a force acts on mass m, then momentum p will be greater than zero. It is this momentum that requires infinite energy to reach light speed. Since infinite energy is not available, mass m cannot reach light speed in this way--and--here is the ironic part: to reach a speed faster than light requires no outside force or energy--just the rest-mass! Albeit, equation 9 shows that superluminal speed is offset by extreme curvature of spacetime. This offset happens instantaneously (yes, more "spooky action at a distance") to ensure that the rest-mass energy is conserved.
Below is a proof that shows the absurdity of assuming it takes a time of r/c seconds for a change of frequency (a change of velocity or mass density) to update a change of wavelength (velocity or curved spacetime), where r is distance and c is the speed of a graviton:
Ironically, the very speed of light itself depends on instantaneous "spooky action at a distance." We can conserve the energy of our two-particle system in the following manner:
The speed of light also depends on the speed of our expanding universe--even if that speed is faster than light:
Equation 19 above shows that velocity Hr could be faster than light; yet the right side of the equation never exceeds c or light speed.
So far, it appears that gravity and dark energy have infinite velocity potential and that spacetime and matter are entangled--which enables "spooky action at a distance" beyond the quantum realm. So ... are there any experiments or observations that lend support to such weirdness? At the time of this writing, I know of no direct observation of superluminal speed. However, black holes lead to the inference that light speed is not enough to escape a black hole's gravity that has a potential meeting or exceeding light speed (see equation 10 above). Additionally, no light can reach us from galaxies that are beyond the cosmological horizon. The "spooky action ..." on a cosmological scale is consistent with astronomical observations cited by Laplace and Van Flandern.
At equation 21 below we define the frequency (f) of an electric field. Albeit, there is a problem. It is assumed that the electric field extends to infinity! At any distance r, an observer allegedly experiences an electric field. If the electric charge q is beyond the cosmological horizon, i.e., r > c/H, an observer at that distance never observes q's electric field nor its frequency f. So at 22 we create a new variable s that equals zero if r > c/H. Equation 23 shows that the observer observes zero evidence of frequency f. Equations 24 through 26 show that variable s should also be applied to gravitational waves (GWs) (and their frequencies), since they are limited to light speed and can't reach an observer if they originate beyond the cosmological horizon.
It is clear that an electric field and GWs have a limited observable range. There is one field, however, that truly has an unlimited range: the vacuum field or "dark energy" if you prefer. An observer at any distance r would never claim there is no evidence of such a field. Thus our new variable s is inapplicable. Velocity v at equation 27 below never equals zero unless r equals zero. At 28 we create a new variable Sv that is always equal to one. As a result equation 29 can be substituted for equation 27.
We bring back the Friedmann equation at 30 below. According to the WMAP spacecraft, space is nearly flat, so we set k to zero.
Let's assume a gravitational field has a limited range of r = c/H. The diagram below shows a sphere with volume V divided into an alpha section and a beta section. The alpha section is within the c/H limit for observer O; the beta section is not. This creates an inequality at 31. If gravity depends on gravitons limited to light speed, the Friedmann equation is invalid if distance r is greater than c/H.
Next, lets assume the vacuum and gravitational fields both exist everywhere. The equality is restored and the Friedmann equation is always valid:
This seems inconsistent with GWs that cannot penetrate the c/H barrier. Let's examine GW equations and see if we can reconcile this apparent inconsistency.
At 33 above we begin with a GW power equation for two rotating black holes. With a little algebra we derive equation 37. At 37 we assume gravity has an unlimited range, so we multiply that part by Sv which equals 1. We further assume GWs that are more than c/H meters away from an observer cannot be detected. So we multiply P and the frequency by s, where s equals 0. Equation 37 confirms that gravity overcomes the c/H barrier and GWs may not. GWs do not carry gravitational information. If there was zero frequency, the black holes would still have gravity and there would be no GWs. The source of GWs is the kinetic energy needed to maintain the orbits of the black holes. Over time this energy is converted to massless waves that propagate no faster than light. Equation 38 below shows how gravity can exist in the absence of GWs (notice that the s's cancel):
<
Conclusion:
It appears that vacuum and gravitational fields extend to infinity unlike the electric field. Both gravity and dark energy have the potential for speed greater than light; yet, ironically, this does not violate the light-speed limit. In fact, the light speed limit itself depends on "spooky action at a distance"--i.e.--entanglement of frequency and wavelength. This entanglement is also essential to the velocity addition formula that ensures that two velocities never exceed light speed.
References:
1. Flanagan, Eanna. Hughes, Scott A. 2005. The Basics of Gravitational Wave Theory. New Journal of Physics.
2. Van Flandern, T. 1999. The Speed of Gravity What the Experiments Say. Meta Research University of Maryland Physics Army Research Lab.
3. Siegel, Ethan. August 30, 2018. Our Motion Through Space Isn't A Vortex, But Something Far More Interesting. Forbes
4. Tzortzakakis, Filippos, LIGO Analysis: Direct Detection of Gravitational Waves. Journal of Research Progress Vol. 1.
5. Roberts, Tom, Schleif, Siegmar. 2007. What is the experimental basis of Special Relativity?
6. Friedmann equations. Wikipedia