ABSTRACT:
By means of two thought experiments and some mathematics this paper shows that extra space dimensions are untenable. This paper also shows that the minimum distance is many orders of magnitude shorter than the Planck length.
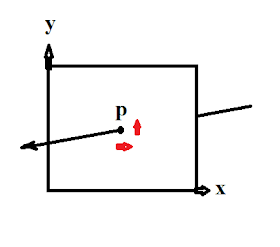
Imagine a 2D universe on an x-y plane (see diagram below). Imagine a normal vector intersecting this plane at point p. 2D-guy inhabits this universe. He can't see the vector that intersects point p. He can only detect point p, so he has no reason to believe the normal vector exists. Now, to avoid point p, he goes around it (see red arrows).
He knows it's possible to draw an imaginary line through point p that can serve as an axis. He also notices when he goes around point p he's not encircling the x-axis or the y-axis--the two dimensions of his space. Thus, he infers that the imaginary axis he's going around does not belong to his 2D universe. He realizes he has discovered a new dimension!
Now, what happens if we apply 2D-guy's process to 3D space? Will we discover a fourth dimension? Let's try it. First we must scale everything up one dimension: The universe becomes 3D; the normal vector becomes a normal plane; Point p becomes line L. Let's assume there's a fourth dimension w, and let's define the normal plane as wx. Plane wx intersects our universe at line L which runs along the x-axis. We should not be able to detect the w-axis nor the bulk of the wx plane. We illustrate this with broken lines at the diagram below:
To avoid line L, we circle around it (see red circular path). We know we can draw an imaginary plane through line L. We know that x is one dimension of the plane. We know the axis we are circling (to avoid line L) is the plane's other dimension. We note we are not going around the x-axis nor the z-axis. That leaves the w-axis, but notice that the w-axis is indistinguishable from the y-axis. Therefore, our assumption that w is a new dimension and is undectable beyond line L is false. Unlike 2D-guy, we have not discovered a new dimension. However, we learned from 2D-guy that if a new dimension exists, it should be possible to do a rotation around an axis that does not exist in our universe. Until someone demonstrates such a rotation, we can conclude, for now, that the highest dimension of space is 3D.
But what if there are extra dimensions that are very small and curled up? If that's the case we should be able to enter alternate universes and those from alternate universes should be able to enter ours. Let me demonstrate what I mean. Imagine a line and pretend it is 3D space. Extending from it is a small extra curled-up dimension:
Let's introduce an arbitrary red object that is way too big to enter the tiny curled-up dimension:
Because the red object is too big to fit, it is assumed there is no way for the big red object to enter or detect the existence of the curled-up dimension. But didn't Euclid say something about a line existing between any two points? (In this case the line would be 3D.)
There's no reason why the big red object can't follow the path of this new line (3D space)and wind up in an alternate universe adjacent to ours:
As you can see, the big red object still can't enter the small, curled-up dimension, but the curled dimension facilitates access to alternate universes. The fact that big objects don't disappear from our universe and don't seemingly emerge from nowhere is strong evidence that microscopic curled-up dimensions don't exist. But wait! Quantum particles pop into existence and vanish all the time. It is hypothetically believed they enter a curled-up dimension (vanish), then leave that dimension and re-enter our universe. However, there's an alternate hypothesis: particles are really particle-waves. Waves experience constructive and destructive interference. When there's an excitation of a field, a particle pops into existence. That excitation could be or is equivalent to constructive interference. When there's destructive interference, energy vanishes--leaving the impression that the particle has disappeared.
The foregoing arguments seem to kill any notion that there are more than three space dimensions, but what about 4D spacetime? Or, what about the 6D object that can be found in Las Vegas? Let's address the 6D object first.
The 6D object I'm referring to is the die. The die has six orthogonal sides. Each side is statistically independent. We can change the value of a side without impacting the value of the other sides. If we change, say, the one to a seven, the other sides will still be two, three, four, five, and six. The most important point we can take away from the die is it is possible to have more than three orthogonal dimensions within 3D space! The die is a 6D object but it is also a 3D cube.
Spacetime, on the other hand, involves three dimensions of space and one dimension of time. If time is multiplied by a velocity, it has units of distance and is treated as a fourth space dimension. But is it really? Let's see what the math has to say:
Equation 1 represents a photon propagating through dimensions x, y, and z over a period of time t. It covers a distance of ct or r. For the sake of keeping the math simple, at equation 2 we rotate the path r so it is along the x-axis. Equation 3 reveals that space and time are not statistically independent, i.e., orthogonal to each other. The the value of time t depends on how far the photon propagates along x, and the value of x depends on how much time t lapses. This is the consequence of converting t into distance units by multiplying it by velocity c. So ct is not a true space dimension that is orthogonal to x. However, time t without c is a very useful statistically-independent parameter. For example, coordinates x, y, z tell you where to be for your dentist appointment and time t tells you when. A change in location does not have to change the time of the appointment, nor does a change in time have to change the location. So what can be done to make ct orthogonal to x? How about multiplying ct and x by factors of g? (See equation 6.) A change in x still causes a change in t, but g-sub-tt can be adjusted so the term stays constant. By the same token, the other term stays constant if g-sub-xx is adjusted when a change in t changes x.
So can we now credibly argue that (g-sub-tt)ct is a genuine fourth space dimension? Well, no 3D space dimension (x,y,z) has to be a function of (depend on) the others. We can, for example, eliminate y and z and still have x. But we can't eliminate a photon's path (x, y and/or z) and still have ct--the distance along a non-existent path. And, if there's no ct, then there's no (g-sub-tt)ct. Therefore, (g-sub-tt)ct is a pseudo-dimension at best.
So far, it seems we've only debunked a fourth dimension of space. What about dimensions five through infinity? Well, how we label a dimension is arbitrary. Any extra dimension can be labeled the fourth dimension. Thus, all arguments we have made against dimension four apply to any extra space dimension.
Now let's turn our attention to the concept of the shortest distance. The popular choice is the Planck length. In fact some theorists quantize space with Planck-size cubes or Planck-size tetrahedrons or Planck-size strings:
In the above diagram, the cube and tetrahedron have sides that are each one Planck length. However, the red diagonal lines reveal shorter lengths all the way down to a single point. These shorter lengths are absolutely necessary to create the shapes desired. Without a zero-length point, for example, there can be no corners for cubes and tetrahedrons. Additionally, there can be no strings in any string theory, since a string is a 1D object. A 1D object implies a zero cross-section or single point. A minimum-distance-greater-than-zero requirement would be a nightmare for M-theorists, since all D-branes would have to be 10 dimensions (including strings!). To have less than 10 dimensions requires zero distance for one or more dimensions. So it can be argued that the minimum distance is really zero, at least on paper. What about the physical world?
Equation 7 tells us that the shortest wavelength is determined by the highest energy. When the universe was a singularity, how short was the singularity's wavelength? If we only account for the energy in the known universe, that wavelength would be approximately a Planck length of a Plank length of a Planck length! Not exactly zero, but far less than a Planck length. Add energy beyond our known universe, and the distance is even shorter.
From a philosophical standpoint, the very concept of length implies a 1D object in the same manner the concept of area implies a 2D object. To measure length requires that we ignore all but one dimension, i.e., we set all but one dimension to zero. So zero distance is necessary, at least in the mind's eye. Since the mind's eye lives in this universe, we can infer that the minimum distance in this universe is zero.
In conclusion, any extra space dimension would allow rotations around an imaginary axis that is not part of 3D space. It would also allow any object access to an alternate universe. The shortest distance is many orders of magnitude shorter than the Planck length, and the Planck length may only be a lower limit of what we can successfully measure.
References:
1. Greene, Brian. 2003. The Elegant Universe. W. W. Norton
2. Irwin, Klee. 04/23/2017. The Tetrahedron. Quantum Gravity Research.
3. Sutter, Paul. 02/23/2022. Loop Quantum Gravity: Does Space-time Come in Tiny Chunks? Space.com








No comments:
Post a Comment