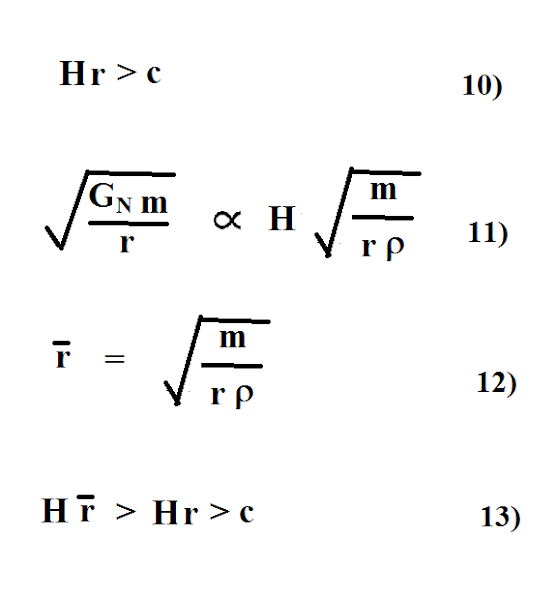Curing Divergences without Supersymmetry and Renormalization

Abstract:

Supersymmetry or ad hoc methods such as renormalization are often used to tame infinities that result from divergent functions in quantum physics. Although SUSY particles have yet to be discovered and may be too massive to fulfill their purpose, and, renormalization seems to lack mathematical rigor. Here we offer an alternative method that employs the least-action and Heisenberg uncertainty principles.

Imagine a Lagrangian with divergent terms. One strategy is to renormalize it. Simply discard the divergent terms, especially if they are infinite. However, Paul Dirac had this to say about such methods: "I must say that I am very dissatisfied with the situation because this so-called 'good theory' does involve neglecting infinities which appear in its equations, ignoring them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves disregarding a quantity when it is small – not neglecting it just because it is infinitely great and you do not want it!"

Another strategy is to add superpartners that each have the same mass as their respective standard-model counterparts but make an opposite contribution to the Lagrangian. As a result, the divergence vanishes. Albeit, there is a slight problem: the symmetry of Super-symmetry is broken--the superpartners are believed to be more massive than their standard-model partners. This deflates the balloon of vanishing divergences. To make matters worse, there is a complete and total lack of empirical evidence supporting these superpartners.

If renormalization seems like bad math and SUSY particles are nowhere to be found, what other options are there? How about the least-action and Heisenberg uncertainty principles? Let's first examine the least-action principle:

A particle typically takes the shortest path possible between two points. For that to happen, delta-s, at equation 1, cannot be a large, divergent quantity. It should be zero units of action or time multiplied by energy. However, the following is true:

Line 3 shows that time multiplied by energy is greater than or equal to h-bar. To get delta-s to equal zero requires steps 4 through 6:

At 7 we set up another substitution. The final equations are 8 and 9 below:

Equations 8 and 9 show why there's a least action principle and why energy is generally conserved. Suppose we have a conserved energy L. The divergent energy, delta-E, can be interpreted as energy borrowed from the vacuum. Because it's borrowed, it must vanish within time delta-t. The larger this energy, the shorter its lifespan. As a result, the energy L that you start with is the energy you end up with. It is conserved. Also, the action is the least action.

At equation 10 we have a Lagrangian where there is no borrowed energy. Because no energy is borrowed, time delta-t is infinite. In other words, this scenario can last indefinitely and create the impression that energy is always conserved.

At equation 11 we have the opposite extreme: a Lagrangian that diverges to infinity. The good news is delta-t is zero, which shows that infinite borrowed energy does not exist. We can also infer that large borrowed energies exist for too short of a time to be meaningfully observed and measured, so the energy we do observe and measure is small by comparison. Thus, renormalization works despite its ad hoc nature because nature wipes out divergences by means of the uncertainty principle and least action. The only time it is appropriate to keep the divergent terms is when divergent energy is added to the system and not borrowed from nothing.

Now, let's suppose L is a Lagrangian for vacuum energy (see equation 12). A Higgs boson (m-sub-H) pops into existence and has a lifespan of t-sub-H. A too-large Higgs mass would have a lifespan too short to provide a meaningful opportunity to observe it, so the mass we are most likely to observe is a smaller mass.

More examples: Equation 13 below takes into account multiple particles. Equation 14 takes into account a Lagrangian or function with multiple terms and parameters.

Since delta-s must be zero to minimize the action, then delta-s along D dimensions must also be zero. Further, both delta-s and s have units of momentum multiplied by position. If we integrate over position and/or momentum space, the following must be true:

The uncertainty of knowing a particle's position is cancelled by knowing its momentum and vice versa. As a result, the particle's action is minimized along with its position path and momentum.

In conclusion, divergences are tamed if the least-action and uncertainty principles are applied. SUSY particles are not needed and ad hoc methods such as renormalization can be set aside.

References:

1. Lincoln, Don. 2013-05-21. What is Supersymmetry? Fermilab.

2. Martin, Stephen P. 1997. A Supersymmetry Primer. Perspectives on Supersymmetry. Advanced Series on Directions in High Energy Physics. Vol. 18.

3. Susskind, Leonard. 2012. Supersymmetry and Grand Unification Lectures. Stanford University

4. McMahon, David. 2008. Quantum Field Theory Demystified. McGraw Hill

5. Baez, John. 11/14/2006. Renormalizability. math.ucr.edu

6. Renormalization. Wikipedia

Giving Neutrinos Mass by Adjusting the Higgs and Electroweak Mathematics

ABSTRACT:

This paper shows a new mathematical algorithm that allows weak-force bosons to have mass and leaves photons massless while giving mass to neutrinos and other leptons.

The right side of equation 1 below is the Higgs vector used to ensure that photons don't have mass and that the weak-force gauge bosons have mass. This same vector also ensures that leptons will have mass except for neutrinos.

Neutrinos, however, are not massless. This fact indicates that the electroweak theory is not complete. To fix the theory we need something like the vector on the right side of equation 2:

This new vector compensates for whatever contributes to neutrino mass. If we use this new vector when determining masses for leptons, and, use the old vector for determining masses for gauge bosons, we end up with the status quo and the extra bonus of slightly massive left-handed neutrinos.

To theoretically justify this new vector we'll examine how the old vector was derived from a Lagrange potential. We will make a minor adjustment to this Lagrange potential without changing its value and its gauge translation invariance. The minor adjustment will allow a derivation of the new vector as well as the old. Here is the Lagrange potential in its original form:

Equations 3 through 6 demonstrate gauge translation invariance and lead to equation 7. Next, we take the derivative with respect to phi to acquire the minimum potentials:

At 11 and 12 above we have the minimum potentials we find in the Higgs vector at equation 1. To derive the new vector at equation 2 we do the following:

Two new terms are added to the potential that cancel each other, so the potential is the same. Once again gauge translation invariance is demonstrated. After all is said and done, we have two useful equations: 18 and 19. If we substitute the zero value at 18 into 19 we have the original Lagrange potential. Once again, we can take the derivative and derive the original Higgs vector. Or, we can take the derivative of equation 19 without the substitution:

At 23 we end up with two non-zero solutions. If phi is small, we have the first approximate solution. If phi is larger we have the second approximate solution. This is consistent with, say, an electron being more massive than its family neutrino. We now have what we need to create the new vector (see equation 2).

The next step is to show how this new vector is applied. When the mathematics is normally done, all terms containing h(x) are discarded at the end, but the solutions don't change if we discard h(x) early or leave it out of the vector. Doing so greatly streamlines the math. Thus the new vector becomes

There are three families of leptons. Since the same mathematics applies to all three, let's just focus on the electron family. The normal interaction Lagrangian for the electron family is

The problem with this Lagrangian is it assumes the left-handed neutrino has no mass, so we need to adjust the Yukawa coupling Ge to G.

Since the right-handed electron doesn't have a corresponding right-handed neutrino, the Greek letter nu with an R subscript has a zero limit at equation 30. After performing the matrix operations we get

Now let's set up some substitutions and define the modified Yukawa coupling G to include neutrino and electron masses:

The final results are below. At 37 we have the left-handed neutrino's mass. At 38 we have the electron's mass (notice how the adjusted Yukawa coupling coupled with the new groundstate equals the standard Yukawa coupling coupled with the original groundstate. Both terms equal the electron's mass.)

The forgoing exercise can be repeated for the other two families of leptons. To account for different masses, simply use different Yukawa couplings.

In conclusion, to give neutrinos mass requires a new Lagrange potential that can yield two field vectors: one for gauge bosons and one for leptons. Also, Yukawa couplings for massive neutrinos need to be added. When these requirements are met, the final solution shows that left-handed neutrinos do indeed have mass.

Quantizing Gravity without the Graviton

Abstract:

This paper shows the connection between "dark energy" and gravity, the equivalence between matter and space, and how gravity works without the graviton or gravitational waves. It also suggests an alternate way to quantize gravity using smaller units--of mass, space and time--than the Planck units.

The same force acting on different masses will cause each mass to move at a different rate: F = ma, where m is mass and a is acceleration. However, the same "gravitational force" causes different masses to fall at the same rate. How can this be? Einstein proposed that when a body appears to be falling to earth, it is really at rest, and the earth is accelerating towards the body at a given rate. Thus the body's mass is irrelevant.

Below is a diagram of Alice who is surrounded by four bodies, including Bob. Bob and the others appear to be either moving away from Alice or towards her, depending on how you follow the arrows. But if we go from left to right, we can think of Alice as the one who is moving away from the surrounding bodies. If we go from right to left, we can think of Alice as the one who is moving towards the surrounding bodies. As a consequence, the surrounding bodies can have any mass and the rate at which Alice and the surrounding bodies diverge or converge will be the same.

Equations 1 and 2 below were derived from Einstein's field equations. Equation 3 was derived from a Friedmann equation where k is set to zero due to spacetime being flat at a large scale where the mass density (rho) is a small number and so is the curvature which is represented by the cosmological constant.

At 4 and 5 we set up a couple of substitutions to be made at 7 and 8 below. Equation 6 shows how mass and space are equivalent. Divide any mass by the vacuum-mass density to get the equivalent volume. Equation 7 shows the universe must expand faster than light as the radius r tends to infinity; otherwise, light speed in a vacuum is not conserved! If both sides of the equation are multiplied by the universe's mass, then the universe's energy is conserved no matter how big or small the universe becomes.

Also, the vacuum-mass density rho correlates with outward pressure, and that pressure is not diminished by an increase in distance r, so the outward pressure continues and so does the universe's expansion. At equation 8 we see that gravity looks similar to equation 7. As the speed of gravity increases, it is offset by the increase in spacetime curvature. As a result, the constant c and energy are conserved.

Equation 9 below shows that gravitational waves are caused by gravity and angular frequency, so they cannot be the cause of gravity. In fact, if angular frequency is zero, there is still gravity but no gravitational waves.

Now, let's imagine Alice and Bob are so far apart that Bob is moving away from Alice faster than light (see 10 below). Alice starts out with very little mass, but decides to go off her diet. As a result, she gains an enormous amount of mass. So much so that she becomes a black hole (see equation 11). The distance between her and Bob is the same but it is now less than Alice's Scharzschild radius. So are Alice and Bob still diverging or are they now converging?

We know that no signal, limited to light speed, ever reached Bob. This includes gravitons, gravitational waves, light, etc. At 12, Alice's mass is converted to it's equivalent space. Finally, the inequality at 13 shows that Bob is still moving faster than light if Alice is at rest, but Alice is no longer at rest--she's moving faster than Bob towards Bob. Thus Alice and Bob are converging as if a "gravitational force" is present.

Take a proton and electron. Equation 14 below shows acceleration depends on both their respective charges, their masses and distance r. Clearly there is an information exchange between them. At equation 15 it's a different story: acceleration only depends on the mass of the proton and distance r. It is clear the two masses don't exchange information. It's as if the proton simply accelerates towards the electron.

Now, let's consider Alice, Bob and Carl below. How fast Alice accelerates depends on the distance of the targets, the targets being Bob and Carl. Surely Alice needs to know the distance of each target so she can adjust her rate of acceleration accordingly?

Consider the diagram below. The numbers in each section add up to the total volume of the 3X3X3 cube. At 17 the volume of each cube is divided by its square. If we multiply each term by the square of Hubble's parameter it becomes apparent that Alice is accelerating less than Bob and Bob is accelerating less than Carl. These three are diverging as if they are in an expanding universe.

Now, let's add mass to the red section. Let's convert it to its equivalent volume which is 100 units. That brings the total to 101 units. Notice that the state of Bob's section (blue) and the state of Carl's section (green) do not change. Each have their previous volume. Also notice that the square areas do not change. This implies no information exchange between Alice, Bob and Carl. But now Alice is accelerating more than Bob and Bob is accelerating more than Carl. The three are converging is if they are in a gravitational field.

The rate of acceleration depends on distance but, as demonstrated above, this does not imply an information exchange between the parties. To drive this point home, imagine we divide up our universe into volume cells, each cell expands at a given rate independently of every other cell. More cells cause a greater rate of expansion, but each cell has no clue how many cells an observer is looking at or what the other cells are doing. The cells exchange no information. Thus the rate of expansion is really up to the observer. Now, suppose you add more volume (cells) to the system without increasing the space. This was done when mass was added to Alice's section (red). Mass's equivalent volume doesn't change the distances between Alice, Bob, and Carl. The result is what we call gravitational acceleration (see equation 20 below). Again, each cell need not know the state of the others. The rate of acceleration depends on the distance the observer chooses to consider.

Now let's turn to quantizing gravity. The popular choice is, of course, the graviton, but the graviton causes a major setback. If we assume the graviton is a real thing, surely we can come up with a reasonable estimate of how many gravitons are in the universe. For example, we could figure the total gravitational energy of the universe and divide that by the average energy of the graviton. At 21 below we plug in the entire mass of the universe to get the gravitational energy, but we don't get units of energy. Instead, we get velocity squared. One could argue that there is no gravitational energy, so there are no gravitons. Equation 22 is an attempt to counter this argument. It uses two masses which give an energy term, but how much gravitational energy there is depends on how much of the universe's total mass we assign to m and m'. Also, whatever gravitational-energy total we arrive at will be exceeded by a single black hole singularity and a single particle that have virtually zero distance between them.

At equation 23 we switch to a smaller scale. We assume the gravitational energy produced by an electron and proton is nEg, where Eg is the energy of one graviton and n is the number of gravitons. Therefore two electron-proton pairs produce 2nEg or 2n gravitons? Not so fast. Since gravitons have energy, they also produce gravitons. At 24 they produce up to an infinite number of gravitons if the distance r limit is zero! So how many gravitons are in the universe? It depends on how you crunch the numbers.

By contrast, it is much easier to estimate how many photons are in the universe, since photons don't produce photons. Electromagnetic energy is a function of charge and not energy or mass. So as long as photons don't have charge, they don't infinitely reproduce themselves. We can take the total luminous energy of the universe and divide it by a photon's average energy to get a reasonable estimate of how many photons there are.

For the above reasons, the graviton is untenable. So then how should we quantize gravity? Gravity is a function of mass (defined as energy divided by light speed squared), space and time. Thus it would make sense to quantize these fundamental dimensions. We could ask, what is the shortest length or time, and, what is the smallest mass? The popular response is, the Planck length, the Planck time and the Planck mass, respectively. But are these really the smallest units? The Planck mass clearly is not the smallest mass. An electron mass is smaller. Also, the Scharzschild radius of an electron is much shorter than a Planck length. The time it takes for a photon to travel the shorter distance is less than the Planck time. So what are the smallest units? Here are the smallest units I have found so far. I call them the Hubble units:

We could take the Hubble length, for example, and quantize equation 13 as follows:

At equation 29 the first term has alpha Hubble lengths; the second term has beta Hubble lengths. The smallest rate of expansion is Hubble's parameter times one Hubble's length. Now, one probable objection to this scheme is space is chaotic and stochastic on the quantum scale, so how can we have such nice, neat units? The Hubble length, for example, could be an expectation value (average) of all the chaotic activity that may make up space. We can think of the Hubble units as perhaps the smallest average units that can be derived from fundamental constants and Hubble's parameter.

In conclusion, unlike the other fundamental interactions, gravity does not appear to have any means for bodies to communicate with each other, nor is communication necessary. Thus the graviton is unnecessary. Further, the graviton fails to conserve energy like its electromagnetic counterpart the photon. A better way to quantize gravity is to quantize space, time and/or mass.

Acknowledgments:

Amber Strunk. Education and Outreach Lead. LIGO Hanford Observatory.

Peter Laursen, Astrophysicist and science communicator at the Cosmic Dawn Center, University of Copenhagen.

References:

1. Parikh, Wilczek, Zahariade. 2020. The Noise of Gravitons. arxiv.org.

2. Feynman, R.P. 07/03/1963. Quantum Theory of Gravitation. Acta Physica Polonica. Vol. XXIV.

3. Graviton. Wikipedia.

4. Carlip, S. 12/1999. Aberration and the Speed of Gravity. arxiv.org.

5. Van Raamsdonk, M. 05/17/2010. Building up spacetime with quantum entanglement. arxiv.org.

6. Hanson, R.; Twitchen, D. J.; Markham, M.; Schouten, R. N.; Tiggelman, M. J.; Taminiau, T. H.; Blok, M. S.; Dam, S. B. van; Bernien, H. (2014-08-01). Unconditional quantum teleportation between distant solid-state quantum bits. Science. 345 (6196): 532–535.

7. Gravitational Wave. Wikipedia.

8. de Rham, C., Tolley, A.J. 03/17/2020. Speed of Gravity. arxiv.org.

9. Carroll, S.M. 12/1997. Lecture Notes on General Relativity. Enrico Fermi Institute.

10. Marsh G.E., Nissim-Sabat. 3/18/1999. Comment on an article by Van Flandern on the speed of gravity. Physics Letters A Vol. 262, pp. 257-260 (1999)

11. Suede M. 11/29/2012. The Speed of Gravity: Why Einstein Was Wrong and Newton Was Right. Blog commentary re: Tom Van Flandern.

12. Cornish N., Blas D., and Nardini, G. 10/18/2017. Bounding the Speed of Gravity with Gravitational Wave Observations. Phys. Rev. Lett. 119, 161102

13. Van Flandern, T. 1999. The Speed of Gravity What the Experiments Say. Meta Research University of Maryland Physics Army Research Lab.

14. Nix, E. 08/22/2018. Who Determined the Speed of Light. History.com.

15. Speed of Gravity. Wikipedia.

16. Tests of General Relativity. Wikipedia.

17. Decross, M. et al. Gravitational Waves. Brilliant.com.

18. Lawden, D.F. 1982. Introduction to Tensor Calculus, Relativity and Cosmology. Dover Publications, Inc.

19. Stefanovich, E. V. 09/16/2018. A relativistic quantum theory of gravity. arxiv.org.

20. Light-time correction. Wikipedia.

21. Liénard–Wiechert potential Wikipedia.

22. Kopeikin, S. M. Fomalont, E. B. 03/27/2006. Aberration and the Fundamental Speed of Gravity in the Jovian Deflection Experiment. arxiv.org.

23. Faber, J. A. 11/24/2018. The Speed of Gravity Has Not Been Measured From Time Delays. arxiv.org.

24. Yin Zhu. 08/18/2011. Measurement of the Speed of Gravity. arxiv.org.

25. Perihelion of Mercury’s Orbit. macmillanlearning.com.

26. Belenchia A, Wald, R.M., Giacomini, F., Castro-Ruiz, E., Brukner, C., Aspelmeyer, M., 03/22/2019. Information Content of the Gravitational Field of a Quantum Superposition. Gravity Research Foundation.

The Faulty Premises of Black-hole Physics

ABSTRACT:

Re: the information paradox. When a theory contains a paradox, it is a clue that one or more premises the theory relies on are faulty. In this paper, we examine the premises, arguments and assumptions that are the foundation of black-hole physics.

All roads lead to Rome. Somewhere in Rome there is a particle trapped in a rotating potential well. Which road (or path) did the particle take to get to Rome? The Heisenberg Uncertainty Principle prevents us from simultaneously knowing the particle's position and momentum. That information could help us determine from whence the particle came.

Prior to being trapped in the potential well, the particle's momentum vector could have given us a sense of direction, but that vector is now rotated. The the information we need is lost. We can't determine the particle's previous positions and momenta, i.e., the road it took to Rome. This is one example of irreversibility that flies in the face of the claim that the state of a particle is always reversible. Yet, it is this claim or premise that leads to the black-hole information paradox.

According to the current paradigm, quantum information is conserved. With perfect knowledge of a particle's current state, it should be possible to trace it backwards and forwards in time. This principle would be violated if information were lost. When information enters a black hole we might assume the information is inside, but then black holes evaporate due to Hawking radiation, and the black hole's temperature is as follows:

As the black hole evaporates, its mass shrinks and its temperature increases. Take note that equation 1 fails to tell us what information went into the black hole, so looking at the final information (remaining mass, momentum, charge) pursuant to the no-hair theorem we can't extrapolate that data backwards and determine what information went into the black hole. It's irreversible. But as shown earlier, irreversibility is not unique to black holes.

Here is yet another example of irreversibility: take two systems, each containing various particles with either positive or negative charge. Coarse grain both systems to get a final result of negative charge for each. The final result is identical for each system; yet, what went into each system varied widely. The final information (negative charge) fails to tell us what went in. A unitary operator would erroneously give the same previous state for each system:

The premise that irreversibility can't and should never happen seems untenable.

Now let's shift our focus to Hawking radiation. If Hawking radiation does not exist, life would be easy. The second law of thermodynamics would never be violated if the black hole maintains or gains mass:

One argument used to justify the existence of Hawking radiation is, "Black holes have temperature; therefore, they radiate." Unfortunately, temperature is not the only variable that determines how much a body radiates. The Stephan-Boltzmann equation below shows that emissivity also plays a role:

The black hole's temperature is irrelevant if the emissivity is zero. And why would the emissivity be zero? Because a black hole's gravity is so strong ... nothing can escape--not even light. Of course, at the quantum scale, there are likely to be events that defy classical physics, but we don't observe them at the macro scale. Apparently, they cancel each other and the classical events are what we observe. So it is not a stretch to assert that a black hole's emissivity is zero (or negative if you count the stuff falling in).

Even if the emissivity is positive, large black holes have a lower temperature than the surrounding environment, so they won't be evaporating any time soon. Small black holes that have a higher temperature probably don't exist, since at least three solar masses are required to create a black hole. Thus, it is no surprise that Hawking radiation has not been observed.

Hawking radiation may also be untenable if the following axiom is true: a system's total mass and temperature emerge from smaller constituents. So the question arises: can a quantum particle pair emerge from parameters such as temperature and total mass? Take note of the following equations:

Equation 4 is consistent with the axiom: a sum of quantum masses make up the total black-hole mass. But at equation 5 we have a pair of radiation particles that depend on the black hole's average temperature which, in turn, depends on the black hole's mass. To sort this out, imagine a single photon at the sun's surface. It's frequency is independent of the sun's average temperature; but the average temperature depends on the photon's frequency along with countless other photons and their frequencies.

To assert that a photon's frequency depends on the temperature is to turn the axiom on its head. Put aside such an assertion and imagine each Hawking particle with its own frequency and other quantum parameters. Together they could be constituents of the black-hole temperature just like the information that entered the black hole. Thus one might be tempted to argue that, at least quantitatively, Hawking radiation preserves the information that entered the black hole. At the very minimum, if black holes evaporate, mass is conserved, so we can justify the following:

Equations 5b and 5c confirm that what leaves the black hole is equivalent to what went in. This may be the inspiration behind another premise: Information is conserved. Really? If it is proportionate to energy, yes. But it is not. It is proportionate to the imaginary surface area A of the event horizon (see equation 3).

Adding a qubit of information to a black hole is done in the following manner:

The result of equations 6 and 7 is one Planck area is added to the surface if a photon with the same wavelength as the Scharzschild radius falls into a black hole. The premise here is the Planck length is the shortest possible length; however, the change-of-Scharzschild radius is shorter than the Planck length if the Scharzschild radius is large (see equation 6). And then there's the sloppy math. Here's the math done properly:

As you can see, at equation 8, there is an extra term added to the Planck-area term, and both terms are multiplied by 8pi. At 9 and 10, The change-of-radius variable is made independent of the Scharzschild radius, and, why not? What are the odds that a particle falling into a black hole will have a wavelength equal to the the Scharzschild radius? Equation 8 shows that the amount of area the particle contributes can vary depending on the size of the Scharzschild radius. If information is proportionate to area, then the amount of information contributed will vary as well. Also, at equation 3, entropy is a function of area. Since entropy must either remain the same or increase, so must information. Information (proportionate to entropy or area) is not conserved!

In conclusion, it is not surprising there is an information paradox, but that paradox is just the tip of the iceberg. It is a clue that one or more premises are flawed. Theorists need to re-examine them. And while they're at it, check the math.

References:

1. Hossenfelder, Sabine (23 August 2019). "How do black holes destroy information and why is that a problem?". Back ReAction. Retrieved 23 November 2019.

2. Hawking, Stephen (1 August 1975). "Particle Creation by Black Holes" (PDF). Commun. Math. Phys. 43 (3): 199–220.

3. Susskind, Leonard (2008-07-07). The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. Little, Brown and Company.

4. Black hole information paradox. Wikipedia.

5. Mathur, Samir D. 03/21/2021. The Elastic Vacuum. Gravity Research Foundation.

6. Chaisson, Eric. Astronomy Today. Englewood, NJ: Prentice Hall, 1993: 503

Is Math Reality?

Is math reality or just a proposed description of reality which may falsely describe, or not accurately or fully describe reality? According to some, the fact that 2 + 2 = 4 is proof that math is reality and vice versa. But what about 2 + 2 = 5? One could argue that this is wrong and fits no reality and isn't real. The counter argument is 2 + 2 = 5 is real (like many string theories) in some parallel universe inside a megaverse.

Unfortunately, there is no empirical evidence of parallel universes--only mathematical evidence. Yet, it is argued that mathematical evidence is every bit as valid as empirical evidence. When these two types of evidence disagree, we simply invent a new universe, i.e., a reality where they do agree. Problem solved?

Hmmmm ..., if math is always right somewhere within a megaverse, wouldn't every crackpot idea be right somewhere within a megaverse? For example, our earth isn't flat, but surely there is some parallel universe that contains a flat earth? It looks as though the scientific method becomes a joke if we are allowed to move the goalpost (invent new unobserved universes) when the math or theory is wrong in this universe.

To claim that math is reality is to ignore infinities--that have never been observed or verified--and negative probabilities (predicted by quantum physics math) and all the instances where the math is wrong, or, where the math is approximate. When calculating the area of a circle, who knows and uses the exact value of pi? No one to my knowledge. If we don't know and can't determine the exact value of pi, then how can we say with confidence that it is real? Our math in general is riddled with approximations and error margins. From an empirical standpoint, we have yet to make a perfect measurement of the circumference of an ellipse or calculate it with a perfect value of pi; yet, some argue that math is reality and reality is math.

The Relativistic Nature of the Expanding Universe

Our expanding universe is not thought to be relativistic. Technically, the galaxies receding away from us are at rest. The space between them is expanding and creating the impression that the galaxies are in motion. However, each galaxy can be treated as a clock, and, it is not likely that any of these clocks tell time at the same rate.

Using the diagram below as a reference, consider Alice and Bob living in a static universe. Alice lives in galaxy A and Bob lives in galaxy B. Each has a photon gun and shoots one photon per second at the other. The vertical red arrows represent the photons fired from one galaxy to the other. When the first photon from Alice (after traveling light years) finally arrives at galaxy B, Bob intercepts it and records it as a unit of time. Since Alice fired photons at regular intervals, Bob only has to wait one second for the next photon and another second for the next one after that and so forth. He receives one photon per second from Alice, and, for similar reasons, Alice receives one photon per second from Bob. This is how Alice and Bob keep track of each other's time rate.

You will note there are some horizontal red arrows at the top of the above diagram. Also located at galaxy A is Gertrude. She also has a photon gun. She fires one photon per second at Alice. Alice therefore intercepts and records one photon per second from Gertrude. Bob also receives photons in the same manner from Norbert who is also lacated at galaxy B (see horizontal red arrows at the diagram's bottom). This is how Alice and Bob keep track of their own time rates.

When the universe is static, both Alice and Bob receive fired photons from all directions at a rate of one photon per second. All clocks seem to agree and equations 1 and 2 provide the relevant math. But suppose the galaxies move away from each other at velocity v due to expanding space. The next diagram represents this scenario:

The vertical red arrows show that the photons take longer to reach their respective destinations and fewer photons are received per second compared to photons represented by the horizontal arrows. Since each photon is counted as a unit of time, Alice and Bob have the impression that the other's time rate is slower. Since Gertrude is located in the same galaxy as Alice, she isn't receding from Alice the way Bob is, so Alice sees no change in her time rate, since she receives the same number of photons (time units) from Gertrude. Ditto for Bob and Norbert at galaxy B.

If we do a little algebra we can derive the Lorentz equation from equation 3 above. The final result is equation 10:

Equation 10 shows each galaxy's proper time (t') shrinking as they accelerate further apart. It does not matter if the galaxies are technically at rest, since the space inbetween and the photons are not at rest. If the space is at rest, here's the result after firing a photon gun for five seconds:

Notice the steady stream of photons. This is where t' = t. The next diagram shows what happens if space expands at a steady rate of v. The photons still have a steady rate but the interval between them has increased, so they are not counted as frequently. Time t' is less than t.

Finally, the next diagram is the most realistic, since the expansion of space is accelerating. Here the the interval between photons continues to grow and they are counted less and less frequently. Time t' is shrinking.

When Alice and Bob are far enough apart, neither will receive any photons from the other. Time t' will be zero. Thus the expanding universe is relativistic if one keeps track of the various time rates at different distances.