Today we are going to work out the quantum mechanics of gravitational waves using my relativity wave function. If you have no clue what I'm talking about, check out my post entitled "The New Relativity Particle Wave Function." The following video provides some basic information on g-waves:
Of course there are always naysayers. Here is a skeptic's video:
I didn't find the magnet demonstration very convincing. Magnets do a great job accelerating iron filings, but not wood chips. If the guy in the above video got those magnets to accelerate something non-metallic, I'd be impressed, but all he did was show magnetic field interactions under a bright light. Thus it seems like a safe bet to build a theory of quantum gravity based on the gravitational wave discoveries.
Below are some gravitational-wave equations we can work with. The first one is the chirp mass (Mc). It depends on two very big masses: m1 and m2. They could be a double-star system or a couple of black holes.
Next we have the scaling amplitude (q)--the size of the wave's stretching and squeezing (here is a link to an animation). Normally, the variable h is used, but later we are going to use h for Planck's constant along with h-bar. G is Newton's constant; c is light speed; distance is d; frequency is f, and there's pi.
Then there is the chirp (dot f). (For a demonstration of the chirp, see the video below .)
Next, we have the gravity-wave phase angle represented by the Greek letter phi. As you can see it depends on time (t). Below it is the chirp waveform amplitude q(t).
We can take q(t) and convert it into a wave-function expression:
As you can see, if we use Euler's identity and add the exponent to its complex conjugate, multiply by 1/2q, we get q(t). We now have a quantum expression we can use.
Since phi is time-dependent, and since the goal is to equate it with the relativity wave function, it is imperative that we make the relativity wave function time-dependent as well:
Note how position variables x, y, z were converted to time variables t1, t2, t3. We add these with t4 and multiply by coefficient a to get the observed time t. The four time dimensions may or may not add up to t which is why we multiply by a. We also multiply kct by A, B and C to make them equal to each expression in the phi function. We add those to get the final result: Dkct=phi(t). We use these equated expressions in the equated wave functions and their complex conjugates below:
Now we have the tools we need to calculate the gravitational waves' energy (E), the entropy (S), the temperature (T), the momentum (p), the velocity (c) and the acceleration due to gravity (g). Let's plug these wave functions into Schrodinger's time-dependant derivative expression and see what happens (but first we need to multiply both sides of the equation above by 2/q and subtract the complex conjugates):
Multiply both sides by a complex conjugate to get the expectation value:
At last! We get the energy (E). With a little algebra we can determine the entropy (S), the temperature (T), the momentum (p). We also get the velocity, which happens to be the speed of light (c). If we divide the velocity by t, we get an acceleration (g).
So there you have it!--a theory of quantum gravity based on something scientists claim they have observed and measured: gravitational waves.




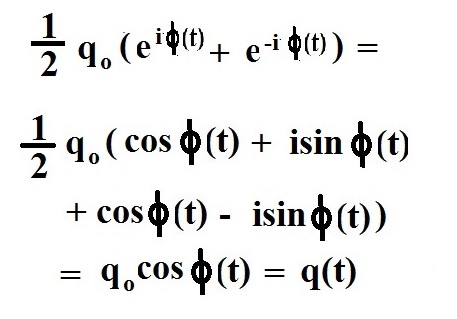







No comments:
Post a Comment