Is it possible to unify quantum physics with Schwarzschild's metric for black holes? Absolutely! All we need to do is adapt my relativity wave function to the task. For more information on the relativity wave function, click here.
Here is an example of the function:
It consists of Euler's identity and more than one k variable (bar-k's to be exact). Time is t; light speed is c, and i is an imaginary number. The variable rs below is the Schwarzschild radius; a and b are terms from the Schwarzschild metric, and r is the radius. Our first step is to transform the bar-k's. For example, bar-k(1) becomes ak(1).
Next, we trade Cartesian coordinates for spherical coordinates. Here is what we get:
We can now express the Schwarzschild metric in quantum mechanical terms:
When the partial derivatives above are solved, we get the standard Schwarzschild metric below:
Looks rather messy. Let's put the variables into a more manageable form:
When the function is used in Schrodinger's time-dependent equation (complete with potential energy V, the Laplacian, and Planck's constant, h-bar), here is what results:
Time to substitute the real values of a and b--but Huston we have a problem! Notice when r is equal to rs, we have zero on the equation's left side and infinity on the right side. The equation works fine as long as the particle is far far away from the black hole's horizon, i.e., when r is a big number. Under those circumstances, the equation reduces to a normal Schrodinger Hamiltonian.
It would also be nice if we had just one momentum term (p). So let's add up the squared momentums (p1, p2, p3). While we're at it, let's subtract the left side from the the right to get energy (E). When the particle is far from the black hole, E should be zero or close to it. As the particle gets closer to the black hole, E increases.


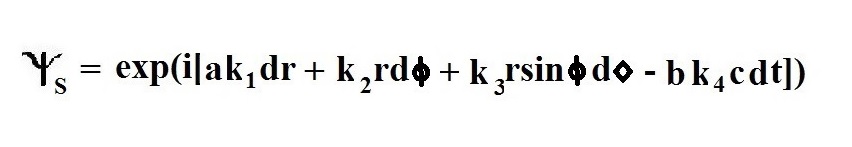






No comments:
Post a Comment