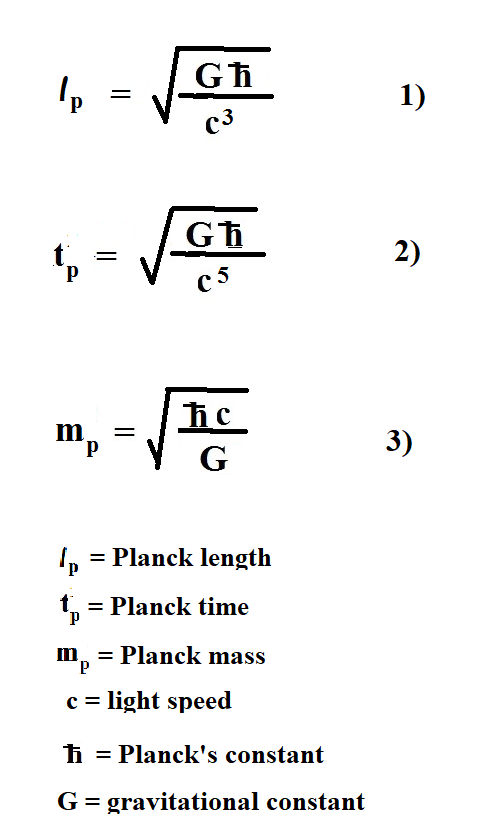How the Gravitational Constant G Destroys Modern Physics

According to all string theories, the Planck length and Planck time are the smallest units. In fact, the string is considered the smallest bit of matter. That brings us to the proverbial question: How long is a string? A string theorist will tell you it is the Planck length. The equations below show the components of the Planck units:

As you can see, the Planck units are made up of the following components: Newton's constant (G), Planck's constant (h-bar) and light speed (c). All these constants are believed to be constant. As long as they are, the Planck units are not just arbitrary units. On the other hand, if one or more of these constants are not always constant ... well that could be a problem.

If we begin with the Lorentz equation, we can derive equation 11 below:

If we assume nothing goes faster than light, then the change in time (delta-t) has an upper limit of t. Also, we know the following is true:

Thus, what follows is also true:

Now, let's assume black holes exist, look what happens when we let radius (r) fall to zero:

The light-speed barrier is broken and energy is no longer conserved. But, then again, if radius r is really small, Heisenberg's uncertainty principle might save the day.

Whoops! Nevermind. A particle, or black hole singularity in this case, can borrow energy from nothing but has to pay it back quickly, in time t. Since the black hole has to borrow more energy than is estimated for the entire universe, it's time is short indeed. The black hole, as we understand it, could not exist. Yet there is a black hole at the center of our galaxy--and it has been there much much longer than time t. How is that possible? Check this out:

If the constant G is allowed to shrink along with radius r, energy is conserved, so the black hole doesn't have to borrow--it can exist as long as it wants. Plus, the light-speed barrier is conserved as well. Unfortunately, the Planck units are arbitrary units. They are not constants of nature.

But does G really shrink? If so, when is it constant and when is it not? If we revisit equation 10, we can derive the following:

Equation 26 shows that delta-t has an upper limit of t but radius r has a lower limit of zero. Since these are components of G, G shrinks to zero as r shrinks to zero. By contrast, equation 27 shows that as r goes to infinity, delta-t goes to zero. As a result, G remains constant. So it appears G is constant at large distances. At small distances, G is no longer constant. For G to be constant at the quantum scale, delta-t needs to grow to infinity as r shrinks to zero. But if that were the case, energy would not be conserved:

Therefore, the gravitational constant G destroys much of modern physics if it remains constant at small scales, and, makes the Planck units arbitrary if it doesn't.

How to Make a Dent in Spacetime for Orbiting Satellites

The above video shows how marbles do elliptical orbits on lycra that is depressed by a massive steel ball. It's analogous to satellites orbiting stars and planets. In this post we show how real spacetime is dented or curved and work out the mathematics of orbiting satellites. So let's define some variables:

Below is diagram D-1. It's a bit crude, but it shall be our guide as we do the math.

Imagine two adjacent volumes of space. Both have volume V. Neither has any significant energy or mass--just empty space. That brings us to equation 1:

Suppose we add a star to one the volumes (see D-1). The star's matter and energy take up some of the space. That leaves a net volume V'. V' is only slightly less voluminous than V, since the star is made of atoms that are mostly space. Suppose the star collapses into a black hole. Surely a black hole takes up no space and V' should equal V. But the black hole and the star have common ground: both have the same energy density within volume V.

At the top of D-1 is the Compton wave formula. When energy (or mass) is added, wavelengths decrease. Shorter wavelengths take up less space and are equivalent to a smaller volume. At D-1, the squiggly lines represent the wavelengths. Note that the top portion (V) has longer wavelengths than the bottom portion (V') If we think of volume in terms of wavelengths, V' is definitely less than V.

The V minus V' average wavelength difference is equivalent to the volume taken up by the star. We can add that volume to V' to get V:

Thus the variables of equation 2 have the same values whether we have energy density in the form of a giant star or a black hole.

Now, let's divide by the z axis (see D-1) to get areas A and A'. Equation 4 gives us the net area (the broken-line rectangle at the center of D-1).

At 5 we divide the areas by the square of the average relative time it takes for a satellite to go along the x and y axes. At 6 through 8 we find the squared velocity of the satellite. It is small compared to light speed--due to gravity being weak ... and ... gravity is weak due to the minor difference in V and V'.

Equation 7 is illustrated at D-2 and D-3 below. Due to increasing energy density (shorter wavelengths), when particle-waves move toward the star, they gain momentum (or lose less momentum). Due to decreasing energy density (longer wavelengths), when particle-waves move away from the star, they lose momentum (or gain less momentum). Thus, on average, the particle waves that make up our satellite, spacetime, etc., are attracted to the star.

At D-3, the long arrows represent the increasing momentum of stuff coming in. The short arrows represent the decreasing momentum of stuff going out.

The converging arrows at D-4 represent the net momentum, the dent in the lycra--the gravitational field. Its intensity increases as the satellite falls due to increasing energy density.

At 10 through 12 we work the star's mass and momentum into the equation. Whenever mass is included in the field, so is it's inertia. Inertia cancels mass and thus different masses fall at the same rate, so we divide by mass as well as multiply.

At 13 through 16 we convert the mass and momentum into n units of Planck mass and Planck momentum.

At 17 we borrow from Heisenberg's uncertainty relations and write the Planck mass in terms of Planck's reduced constant. We make a substitution at 18. At 19 we convert the reciprocal of the Planck momentum squared and make another substitution at 20. Some variables cancel each other.

At 20 we have something close to what we need. All that's left to do is to put the variables back in that we took out earlier (for ease of computation):

At last! We have equation 24. It gives us the satellite's instant velocity at any point during its orbit. Equation 23 allows us to change the ellipse coefficient so we can have a variety of elliptical orbits (see D-5 below) on the dented lycra of spacetime.

Update: Below is a formal proof showing that equation 2 is a solution of Einstein's field equations.

Update: How much actual space does a black hole occupy? It has a singularity with a zero-limit radius (r), but a physical extent of radius (rs), the Scharzschild radius. The answer appears to be a volume with the Schwarzschild radius. Below is the mathematics showing how a black hole takes up space: