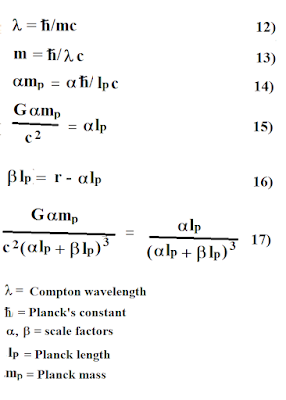Why Entanglement and Faster Than Light Speed Are Consistent with Relativity

ABSTRACT:

This paper shows why entanglement is not limited to the quantum realm, and shows how entanglement and superluminal speed is not only possible, but consistent with special and general relativity.

Imagine two photons. Photon A and photon B are propagating in opposite directions. According to the velocity addition formula, their combined velocity v is as follows:

Now, imagine two observers, Alice and Bob. Alice looks at each photon individually and notices that they each propagate at c. Bob looks at both photons at once and notes that their combined velocity is c. At this point, you probably have some questions: How does photon A seem to know that photon B is propagating in the opposite direction? It's not like photon B can send a signal to photon A (a signal that would have to be faster than light) to let photon A know that it needs to cut its velocity in half along with photon B so their combined velocity will be no faster than light. Further, how do A and B seem to know that Bob is watching them both? They also seem to know that Alice is watching only one of them. The one she's watching seems to adjust its velocity to c just for her benefit. It's as if the photons are entangled with each other and also entangled with all observers.

Einstein described quantum entanglement as "spooky action at a distance"--yet, where would the velocity addition formula be without "spooky action at a distance"? Below is a mathematical derivation of the entanglement of two particles with velocities v1 and v2:

Equation 7 above shows that, at any distance r (the distance between the two particles), any change of velocities (v1, v2) must lead to an instantaneous change in velocity v; otherwise, light speed c would not be constant in a vacuum. Note that the terms on the right side are in units of frequency and wavelength. To maintain a constant light speed requires any change of frequency to be instantly offset by a change of wavelength. Additionally, this entangled relationship between frequency and wavelength is shown by equation 9 below:

At 11 above is a scalar version of Einstein's field equations. Equation 10 shows that velocity v can be infinite if distance r drops to zero. How is this possible given that infinite energy is required to accelerate mass m to light speed? Equation 9 provides the answer: the infinite velocity is achieved with just the rest-mass energy (E). No force acts on mass m. If a force acts on mass m, then momentum p will be greater than zero. It is this momentum that requires infinite energy to reach light speed. Since infinite energy is not available, mass m cannot reach light speed in this way--and--here is the ironic part: to reach a speed faster than light requires no outside force or energy--just the rest-mass! Albeit, equation 9 shows that superluminal speed is offset by extreme curvature of spacetime. This offset happens instantaneously (yes, more "spooky action at a distance") to ensure that the rest-mass energy is conserved.

Below is a proof that shows the absurdity of assuming it takes a time of r/c seconds for a change of frequency (a change of velocity or mass density) to update a change of wavelength (velocity or curved spacetime), where r is distance and c is the speed of a graviton:

Ironically, the very speed of light itself depends on instantaneous "spooky action at a distance." We can conserve the energy of our two-particle system in the following manner:

The speed of light also depends on the speed of our expanding universe--even if that speed is faster than light:

Equation 19 above shows that velocity Hr could be faster than light; yet the right side of the equation never exceeds c or light speed.

So far, it appears that gravity and dark energy have infinite velocity potential and that spacetime and matter are entangled--which enables "spooky action at a distance" beyond the quantum realm. So ... are there any experiments or observations that lend support to such weirdness? At the time of this writing, I know of no direct observation of superluminal speed. However, black holes lead to the inference that light speed is not enough to escape a black hole's gravity that has a potential meeting or exceeding light speed (see equation 10 above). Additionally, no light can reach us from galaxies that are beyond the cosmological horizon. The "spooky action ..." on a cosmological scale is consistent with astronomical observations cited by Laplace and Van Flandern.

At equation 21 below we define the frequency (f) of an electric field. Albeit, there is a problem. It is assumed that the electric field extends to infinity! At any distance r, an observer allegedly experiences an electric field. If the electric charge q is beyond the cosmological horizon, i.e., r > c/H, an observer at that distance never observes q's electric field nor its frequency f. So at 22 we create a new variable s that equals zero if r > c/H. Equation 23 shows that the observer observes zero evidence of frequency f. Equations 24 through 26 show that variable s should also be applied to gravitational waves (GWs) (and their frequencies), since they are limited to light speed and can't reach an observer if they originate beyond the cosmological horizon.

It is clear that an electric field and GWs have a limited observable range. There is one field, however, that truly has an unlimited range: the vacuum field or "dark energy" if you prefer. An observer at any distance r would never claim there is no evidence of such a field. Thus our new variable s is inapplicable. Velocity v at equation 27 below never equals zero unless r equals zero. At 28 we create a new variable Sv that is always equal to one. As a result equation 29 can be substituted for equation 27.

We bring back the Friedmann equation at 30 below. According to the WMAP spacecraft, space is nearly flat, so we set k to zero.

Let's assume a gravitational field has a limited range of r = c/H. The diagram below shows a sphere with volume V divided into an alpha section and a beta section. The alpha section is within the c/H limit for observer O; the beta section is not. This creates an inequality at 31. If gravity depends on gravitons limited to light speed, the Friedmann equation is invalid if distance r is greater than c/H.

Next, lets assume the vacuum and gravitational fields both exist everywhere. The equality is restored and the Friedmann equation is always valid:

This seems inconsistent with GWs that cannot penetrate the c/H barrier. Let's examine GW equations and see if we can reconcile this apparent inconsistency.

At 33 above we begin with a GW power equation for two rotating black holes. With a little algebra we derive equation 37. At 37 we assume gravity has an unlimited range, so we multiply that part by Sv which equals 1. We further assume GWs that are more than c/H meters away from an observer cannot be detected. So we multiply P and the frequency by s, where s equals 0. Equation 37 confirms that gravity overcomes the c/H barrier and GWs may not. GWs do not carry gravitational information. If there was zero frequency, the black holes would still have gravity and there would be no GWs. The source of GWs is the kinetic energy needed to maintain the orbits of the black holes. Over time this energy is converted to massless waves that propagate no faster than light. Equation 38 below shows how gravity can exist in the absence of GWs (notice that the s's cancel):

<

class="separator" style="clear: both;">

Conclusion:

It appears that vacuum and gravitational fields extend to infinity unlike the electric field. Both gravity and dark energy have the potential for speed greater than light; yet, ironically, this does not violate the light-speed limit. In fact, the light speed limit itself depends on "spooky action at a distance"--i.e.--entanglement of frequency and wavelength. This entanglement is also essential to the velocity addition formula that ensures that two velocities never exceed light speed.

References:

1. Flanagan, Eanna. Hughes, Scott A. 2005. The Basics of Gravitational Wave Theory. New Journal of Physics.

2. Van Flandern, T. 1999. The Speed of Gravity What the Experiments Say. Meta Research University of Maryland Physics Army Research Lab.

3. Siegel, Ethan. August 30, 2018. Our Motion Through Space Isn't A Vortex, But Something Far More Interesting. Forbes

4. Tzortzakakis, Filippos, LIGO Analysis: Direct Detection of Gravitational Waves. Journal of Research Progress Vol. 1.

5. Roberts, Tom, Schleif, Siegmar. 2007. What is the experimental basis of Special Relativity?

6. Friedmann equations. Wikipedia

Why the Speed of Gravity and the Speed of Gravitational Waves Are Not the Same

ABSTRACT:

According to Relativity Theory, everything propagates through spacetime at light speed. However, a mass at rest propagates solely through time and experiences zero velocity. A massless photon propagates solely through space and experiences no time. Other objects propagate through time and space, and, experience both time and subluminal velocities. This paper demonstrates that both gravity (the fundamental interaction) and gravitational waves propagate at light speed through spacetime, but with varying degrees through time and space, i.e., they each have different velocities through space.

The year was 1971. Via the Apollo 15 mission, David Scott performed the following experiment on the moon: With a hammer in one hand and a feather in the other, he held them the same distance from the moon's surface. He dropped them. They hit the ground simultaneously. This experiment might not seem like a big deal, but it confirms that Galileo was correct. More importantly, it shows that gravitational interactions (with the exception of gravitational waves) should never be modeled after the electromagnetic (EM) force.

The EM force, like Newtonian forces, conserves energy, momentum and itself in the following manner:

Equations 1 and 2 above show that different masses have different velocities and different rates of acceleration when acted on by the same magnitude of force. Since momentum is conserved, we can use equations 2 above and 3 below to predict the speed of the photons that mediate the force:

No surprises here. Photons propagate at c as expected. Gravity, unlike EM, is full of surprises. Let's model gravity after the EM force and see what happens. Let's assume there is a gravitational field of gravitons that mediate the "force" of gravity. Here is the math:

At 6 and 7 above, force and momentum are not conserved. If we assume momentum is conserved, at 8 the speed of gravitons depends on the mass of the falling object. We cannot count on their speed being c. What about gravitational waves? Why do they consistently propagate at or near the speed of light? Consider the following thought experiment:

You throw a baseball with enough force to place it into orbit around the earth. The force you use is independent of and counters gravity. It is also conserved and so is the ball's angular momentum. The ball's tangential velocity depends on its mass and vice versa. As the ball orbits earth its velocity changes, i.e., the ball accelerates. An accelerating mass emits gravitational waves (GWs). The energy converted to GWs is the same conserved energy you put into the ball when you threw it into orbit. We can predict the speed of these GWs the same way we predicted the speeds of photons and gravitons:

Equation 9 shows that the ball's velocity happens to equal the gravitational potential velocity at distance r. If the ball had more mass (m), its velocity would be less and its orbit would decay. If the ball had less mass, it would have more velocity and would rise out of orbit. Equation 10 shows how much power P is emitted. Over time velocity v will be reduced and the ball will spiral into the earth. At any time, momentum p equals mv. Equation 11 predicts the speed of GWs to be ~c, the speed of light. This is possible because the baseball was originally accelerated to v by you, not gravity. To predict the speed of gravity, absent the influence of another force (you throwing a baseball), requires a model that is different from the EM or force model. Over a century ago, Einstein realized this and had a big idea:

From an airplane flying 10,000 feet above the earth's surface, drop several items with different masses. If we assume they are falling to earth, they all fall at the same rate, so momentum at any instant is not conserved. But what if those items are at rest and it is the earth with mass M falling or accelerating to the items? Clearly, an independent force accelerating the earth would be conserved. With more mass, the earth would accelerate less. The problem is, with more mass the earth really accelerates more. This fact implies that there is no independent force causing earth to accelerate. So there is apparently no independent force acting on the earth or the items that appear to be falling.

If the earth simply accelerates to the items, what need is there for a graviton? As shown at 6 through 8 above, gravitons, if they exist, fail to either conserve force, energy and momentum, or, they don't have a consistent speed if force, energy and momentum are conserved. David Scott's experiment showed us this is true. The feather and the hammer fell at the same rate, not different rates.

Laplace and Van Flandern, based on observations, concluded that the speed of gravity must be several orders of magnitude faster than light. Perhaps infinite! (Masses simply accelerating towards one another combined with independant forces causing angular momentum could certainly provide that impression.) Other physicists hate the idea of infinite speed and insist the speed of gravity is c. To accommodate the Laplace and Van Flandern observations, they point to a model of moving charges, where one charge's vector is lined up with the another charge's instant position rather than its retarded position, creating the illusion that there is no light-time delay, i.e., infinite photon speed when in reality photon speed is c. This model is then projected onto a cosmological scale, and thus moving planets and stars work in a similar fashion and create the illusion of infinite graviton speed when in reality graviton speed is allegedly c. The problem with this model is it completely ignores the Heisenberg Uncertainty Principle. For the model to work, one has to know the position and velocity of the charges with precision. And, as demonstrated above, charges (or EM) conserve force and momentum in a way that gravity does not.

Laplace, Van Flandern and the physicists who criticize them have one thing in common: they all think of gravity as a force consisting of bosons that either propagate at c or much faster than c. Because of General Relativity, it makes perfect sense that most physicists want to limit the speed of gravity to c; however, when two black holes collide and form a new more massive singularity, it is not clear how a boson propagating at c can escape that singularity and inform the rest of the universe of the event. Since nothing propagating at c can escape a black hole, how does this new black hole singularity reset the curvature of its surrounding spacetime?

Let's start with what we know. At 12 below we have the Compton wavelength equation. Note that when mass m changes, the wavelength must change instantaneously, since a mass and its wavelength are essentially the same entity. If we think of the wavelength as spacetime, then spacetime is updated the instant mass changes. At 14 we convert the equation to Planck units with an alpha scale factor. At 15 we derive a Scharzschild radius. Equation 16 shows that a change in alpha instantaneously causes a change in beta, since their sum times a Planck length make up distance r. (Distance r, of course, along with the mass, determines the rate of Newtonian acceleration.) Equation 17 is a scalar version of Einstein's field equations. On the right side we have curvature units.

When two black holes merge, alpha increases everywhere it appears at equation 17. This causes an instantaneous decrease of beta at any distance r from the new black hole's singularity. Thus the new black hole doesn't have to send information at light speed or any speed to update its surrounding spacetime. Mass and spacetime have an entangled relationship. Energy and momentum equations show this to be true. Where would energy and momentum be without mass entangled with velocity? Of course velocity is in units of space and time. Thus one can conclude that the only valid speed for gravity is how fast matter moves at an arbitrary distance from a falling observer:

Equation 18 above shows how fast gravity moves through space. Equation 19 shows how fast gravity moves through time. Finally, equation 20 shows how fast gravity moves through spacetime--the speed of light.

References:

1. Ibison, Michael, Puthoff, Harold E., Little, Scott. The Speed of Gravity Revisited.

2. Kopeikin, Sergei, Fomalont, Edward B. 27 Mar 2006. Aberration and the Fundamental Speed of Gravity in the Jovian Deflection Experiment.

3. Flanagan, Eanna. Hughes, Scott A. 2005. The Basics of Gravitational Wave Theory. New Journal of Physics.

4. Carlip, S. Aberration and the Speed of Gravity. December 1999.

5. Van Flandern, T. 1999. The Speed of Gravity What the Experiments Say. Meta Research University of Maryland Physics Army Research Lab.

6. Siegel, Ethan. August 30, 2018. Our Motion Through Space Isn't A Vortex, But Something Far More Interesting. Forbes

7. Galileo's Leaning Tower of Pisa experiment. Wikipedia.

8. David Scott does the feather hammer experiment on the moon | Science News. Youtube.com

9. Tzortzakakis, Filippos, LIGO Analysis: Direct Detection of Gravitational Waves. Journal of Research Progress Vol. 1.