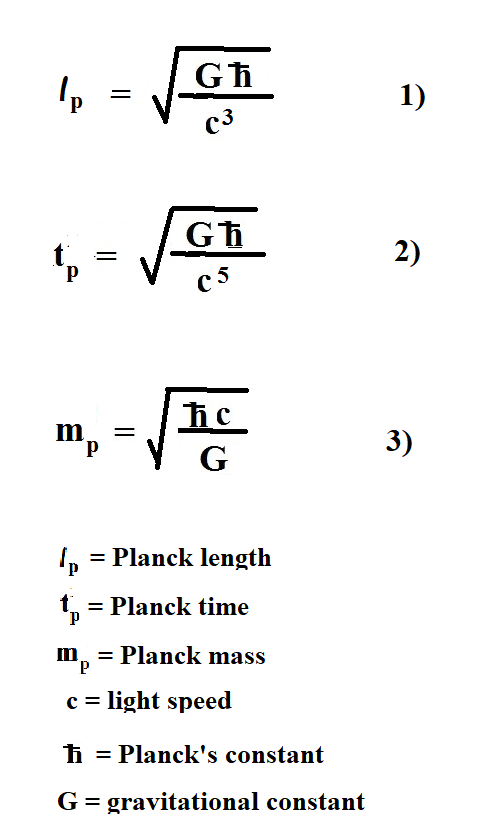How the Gravitational Constant G Destroys Modern Physics

According to all string theories, the Planck length and Planck time are the smallest units. In fact, the string is considered the smallest bit of matter. That brings us to the proverbial question: How long is a string? A string theorist will tell you it is the Planck length. The equations below show the components of the Planck units:

As you can see, the Planck units are made up of the following components: Newton's constant (G), Planck's constant (h-bar) and light speed (c). All these constants are believed to be constant. As long as they are, the Planck units are not just arbitrary units. On the other hand, if one or more of these constants are not always constant ... well that could be a problem.

If we begin with the Lorentz equation, we can derive equation 11 below:

If we assume nothing goes faster than light, then the change in time (delta-t) has an upper limit of t. Also, we know the following is true:

Thus, what follows is also true:

Now, let's assume black holes exist, look what happens when we let radius (r) fall to zero:

The light-speed barrier is broken and energy is no longer conserved. But, then again, if radius r is really small, Heisenberg's uncertainty principle might save the day.

Whoops! Nevermind. A particle, or black hole singularity in this case, can borrow energy from nothing but has to pay it back quickly, in time t. Since the black hole has to borrow more energy than is estimated for the entire universe, it's time is short indeed. The black hole, as we understand it, could not exist. Yet there is a black hole at the center of our galaxy--and it has been there much much longer than time t. How is that possible? Check this out:

If the constant G is allowed to shrink along with radius r, energy is conserved, so the black hole doesn't have to borrow--it can exist as long as it wants. Plus, the light-speed barrier is conserved as well. Unfortunately, the Planck units are arbitrary units. They are not constants of nature.

But does G really shrink? If so, when is it constant and when is it not? If we revisit equation 10, we can derive the following:

Equation 26 shows that delta-t has an upper limit of t but radius r has a lower limit of zero. Since these are components of G, G shrinks to zero as r shrinks to zero. By contrast, equation 27 shows that as r goes to infinity, delta-t goes to zero. As a result, G remains constant. So it appears G is constant at large distances. At small distances, G is no longer constant. For G to be constant at the quantum scale, delta-t needs to grow to infinity as r shrinks to zero. But if that were the case, energy would not be conserved:

Therefore, the gravitational constant G destroys much of modern physics if it remains constant at small scales, and, makes the Planck units arbitrary if it doesn't.

How to Make a Dent in Spacetime for Orbiting Satellites

The above video shows how marbles do elliptical orbits on lycra that is depressed by a massive steel ball. It's analogous to satellites orbiting stars and planets. In this post we show how real spacetime is dented or curved and work out the mathematics of orbiting satellites. So let's define some variables:

Below is diagram D-1. It's a bit crude, but it shall be our guide as we do the math.

Imagine two adjacent volumes of space. Both have volume V. Neither has any significant energy or mass--just empty space. That brings us to equation 1:

Suppose we add a star to one the volumes (see D-1). The star's matter and energy take up some of the space. That leaves a net volume V'. V' is only slightly less voluminous than V, since the star is made of atoms that are mostly space. Suppose the star collapses into a black hole. Surely a black hole takes up no space and V' should equal V. But the black hole and the star have common ground: both have the same energy density within volume V.

At the top of D-1 is the Compton wave formula. When energy (or mass) is added, wavelengths decrease. Shorter wavelengths take up less space and are equivalent to a smaller volume. At D-1, the squiggly lines represent the wavelengths. Note that the top portion (V) has longer wavelengths than the bottom portion (V') If we think of volume in terms of wavelengths, V' is definitely less than V.

The V minus V' average wavelength difference is equivalent to the volume taken up by the star. We can add that volume to V' to get V:

Thus the variables of equation 2 have the same values whether we have energy density in the form of a giant star or a black hole.

Now, let's divide by the z axis (see D-1) to get areas A and A'. Equation 4 gives us the net area (the broken-line rectangle at the center of D-1).

At 5 we divide the areas by the square of the average relative time it takes for a satellite to go along the x and y axes. At 6 through 8 we find the squared velocity of the satellite. It is small compared to light speed--due to gravity being weak ... and ... gravity is weak due to the minor difference in V and V'.

Equation 7 is illustrated at D-2 and D-3 below. Due to increasing energy density (shorter wavelengths), when particle-waves move toward the star, they gain momentum (or lose less momentum). Due to decreasing energy density (longer wavelengths), when particle-waves move away from the star, they lose momentum (or gain less momentum). Thus, on average, the particle waves that make up our satellite, spacetime, etc., are attracted to the star.

At D-3, the long arrows represent the increasing momentum of stuff coming in. The short arrows represent the decreasing momentum of stuff going out.

The converging arrows at D-4 represent the net momentum, the dent in the lycra--the gravitational field. Its intensity increases as the satellite falls due to increasing energy density.

At 10 through 12 we work the star's mass and momentum into the equation. Whenever mass is included in the field, so is it's inertia. Inertia cancels mass and thus different masses fall at the same rate, so we divide by mass as well as multiply.

At 13 through 16 we convert the mass and momentum into n units of Planck mass and Planck momentum.

At 17 we borrow from Heisenberg's uncertainty relations and write the Planck mass in terms of Planck's reduced constant. We make a substitution at 18. At 19 we convert the reciprocal of the Planck momentum squared and make another substitution at 20. Some variables cancel each other.

At 20 we have something close to what we need. All that's left to do is to put the variables back in that we took out earlier (for ease of computation):

At last! We have equation 24. It gives us the satellite's instant velocity at any point during its orbit. Equation 23 allows us to change the ellipse coefficient so we can have a variety of elliptical orbits (see D-5 below) on the dented lycra of spacetime.

Update: Below is a formal proof showing that equation 2 is a solution of Einstein's field equations.

Update: How much actual space does a black hole occupy? It has a singularity with a zero-limit radius (r), but a physical extent of radius (rs), the Scharzschild radius. The answer appears to be a volume with the Schwarzschild radius. Below is the mathematics showing how a black hole takes up space:

How A Mass-less Gluon Can Have A Finite Range

According to the textbooks and many online sources, the range of a boson is determined by its mass. For example, a photon has an unlimited range due to its lack of mass. The W bosons have mass and thus have a limited range. Then there's the gluon, a mass-less boson with a finite range. How is that possible? That's what we will explore in this post. First, let's define the variables we will be using:

Starting with the Klein-Gordon equation, we derive the range equation (see equation 5 below).

We can also derive the range equation if we start with Einstein's famous equation:

At equation 13 above, we plug in a gluon's zero mass and get an infinite range. Not good! So what's wrong with this equation? For one, it strongly resembles the Compton or De Broglie wavelength formula. Calculating a particle-wave's wavelength is not the same as calculating its range. The two concepts might overlap some of the time, but not all of time. For example, photons can have different wavelengths but all of them have the same range. What we really found at 13 is a particle wavelength with zero energy/c^2--it's an infinite wavelength. Coincidentally, it's a photon's range.

OK, so how to we fix this equation? We derive the missing variable alpha. Equation 18 below is Newton's force equation, which is derived from the range equation. Notice that the acceleration (c/t) is fixed. Variable c is constant, so is t, since t was pulled out of Planck's constant (h-bar). Acceleration should vary, so we add the alpha coefficient to get the proper Newton equation. From there we derive Hooke's equation at 23.

Hooke's equation sort of behaves like the strong force or a rubber band. As range x increases, so does the force. Now let's work backwards and re-derive the range equation (see 25 below). At equations 26, 27, 28, we test our new range equation with particles of varying masses and accelerations.

At 26 the gluon's range is limited if its mass is zero and its acceleration is infinite. At 27, the photon has unlimited range due to zero mass and zero acceleration. At 28, the bowling ball has infinite range in a friction-less environment if it has zero acceleration. Newton would be proud!

Now, re: the qluon, does it really have infinite acceleration? To explore this question, let's go back to Newton's equation and derive equation 30 below:

At equation 30 we have light speed (c) divided by time (t). Nothing can go faster than light, so how can there be infinite acceleration? We know that a constant tangential velocity going around a circle, or oscillating is a form of acceleration, since acceleration is change of direction as well as change of speed. At equation 31 below, acceleration (a) goes to infinity as radius x goes to zero. At 32 to 34 we convert x into time (t).

At 34 above acceleration (a) goes to infinity as time (t) goes to zero. So why would time go to zero? We know that a photon going light speed experiences no time. A gluon going light speed would also experience no time. Being confined to the nucleus, its displacement velocity could be less than c, but it's oscillation velocity is c if it is a mass-less particle. At 35 to 38 we set alpha equal to the Lorentz factor.

We plug c^2 into the Lorentz factor and get a value of infinity for alpha or 1/0. We plug this into equation 40, do a little math, and get infinite acceleration at 42.

Equation 42 states the following: Given a fixed amount of energy (E), zero mass, and infinite acceleration (due to zero time and strong interactions), the range (x) of the gluon is limited. Equations 43, 44 support this statement. Equation 45 shows that the range of a particle is simply its energy divided by the force (F).

The gluon's force is zero mass times infinite acceleration. If we multiply this force by time we get a momentum. Just for fun, let's set this momentum equal to mc (see 47). If we plug mc into the range equation (48), something cool happens.

After plugging in some numbers we get the mass of a nucleon (proton, neutron) at 51. We start with a mass-less gluon and end up with something with mass within the limited range of the nucleus.

Below, we go back a few steps and do the math for a photon. As expected, it has infinite range.

The key difference between the photon and the gluon is revealed at 53 above. In the photon's case, the zero Lorentz factor is coupled with the mass instead of the acceleration. This leads to zero mass times zero acceleration times an infinite distance equals a fixed amount of energy.

A Simple Schrodinger-Equation Solution for the Periodic-Table Elements

Suppose you want to solve Schrodinger's equation for the hydrogen atom. It's the simplest atom in the universe: only one proton and one electron, so finding the solution should be as easy as blowing up a hydrogen balloon, right? Here's an operation Schrodinger's equation requires you to perform:

Three partial derivatives with respect to spherical coordinates of the function psi. That doesn't sound too bad, but take a look at the function psi:

Obviously it's going to take you more than a minute to find a solution. Looking at the function above, it is no surprise many QM books never take you past the hydrogen atom. To find the ionization energies of all the atoms in the periodic table seems like a daunting task, requiring a supercomputer. But there is a quick-and-dirty way to achieve the task with no computer help. However, it requires that we simplify the wave function.

Often, the basis chosen for the wave function involves space coordinates, but the basis we will choose is going to be time or space-time.

Equations 1 and 2 show how a single dimension (ct or x4) subsumes all three space dimensions and time. This will allow us to do one double derivative of the function instead of the more complicated Laplacian operation.

At 3 below we express the Schrodinger equation using the space-time variable (x4).

Here is the wave function:

At 5 we choose a value for the wave number (k). At 6 we solve the kinetic-energy term and convert the units to electron volts.

At 7 through 11 we solve the potential-energy term (V):

We put all the terms together and do the math. At the other end the solution comes out (see equation 22):

Finding the ground-state ionization energy for hydrogen is now just a plug-n-chug operation:

With our new Schrodinger solution, we can easily find the ionization energy for more complicated atoms such as carbon:

The main trick is finding the values for constants A, B, and C. Here they are for atoms with up to 12 electrons:

OK, so how do we find A, B, and C? Let's take a real-world example. We want to find the values of A, B, and C for atoms with at least 13 electrons. The smallest of which is Aluminum (Al). We look at some data (click here to see the data) and choose a sample size of five elements (Z >= 13). We then make a pretty little table:

Notice as the table progresses downward it represents the equivalent of taking a double derivative of the energies. Notice at the last row, the values are pretty similar, around 3.5. Let's figure out the average:

Let's take the integral of the average with respect to Z, and then find B:

Notice we didn't use the integer Z values to find B. We used 13.5, 14.5, etc. That's because we used the numbers in the second to the last table row. If you follow the broken lines leading to the top of the table, they fall half way between the Z values. We are dealing with energy differences and not the energies themselves. Each energy difference corresponds to a half-way point.

Now that we know B, let's do another integral to find A:

Let's not forget C. This time we are dealing with the energies and not energy differences, so we plug in the integer Z values:

And here's our final answer:

We should check this against the database (click here for data) for every 13th electron listed. We may have to tweak A, B and C a little to get a near-perfect fit.