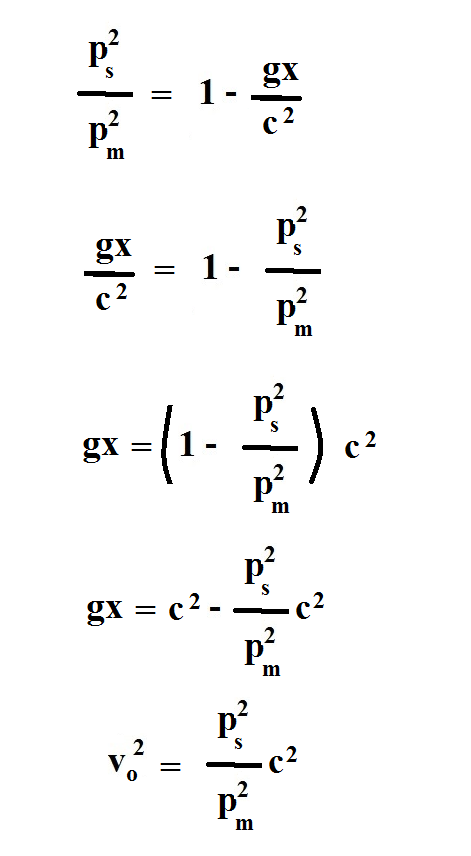Using Fluid Mechanics to Explain Expanding Spacetime and Gravity

The above video is an excellent demonstration of Bernoulli's principle. Notice how the current flows to the right and how the leaves get caught in the eddies. The current is slowed by the obstacles and this causes a back flow. Now imagine a current of expanding spacetime flowing in all directions, and matter swirling in eddies we call galaxies. The outward flow is slowed by the presence of matter--there is a back flow we call gravity.

Below is Bernoulli's equation along with a couple of diagrams. The top diagram shows a boat going merrily down an unimpeded stream. Pressure (P) is zero. This is analogous to an expanding universe devoid of matter. The second diagram shows a stream with a big black boulder in the way. It slows the stream down. The current pushes and brushes the boulder, so pressure (P) is greater than zero. There is a back flow indicated by the red arrow. The boat is pushed upstream to the boulder. This is analogous to matter in an expanding universe causing a gravitational effect.

Bernoulli's equation isn't very practical if applied to spacetime and gravity. Bernoulli didn't take into account relativity, for instance. However, we learn a very useful concept from Bernoulli: Mass causes pressure to rise and the current velocity (v) to slow. If pressure falls, velocity increases, but in this case, pressure can only fall if mass is reduced. Kind of sounds like momentum conservation, doesn't it?

In the diagram below we feature a momentum equation. If spacetime were devoid of all matter, the outflow velocity (v) would equal the back flow velocity (c) (see arrows). The mass pressure density (pm) would equal the vacuum mass density (ps). There would be no gravity--just expansion.

The next diagram shows a universe with a black hole. Expanding spacetime flows around and puts pressure on this black hole. To conserve momentum, the outflow velocity is reduced. The result is a back flow indicated by the arrows in red. We have gravity.

The momentum equation seems like a pretty good model for spacetime and gravity, but is it valid? Let's see if we can prove its validity. First let's define some variables:

And here's the proof:

Within the proof we derived another useful equation:

The above equation tells us the instant gravitational velocity squared (gx) at a given location (x)--or, fluid-mechanically speaking, the net back flow rate squared.

Update: The following proof shows that spacetime momentum is conserved but gravitational momentum is not:

The first equation above clearly shows that any change to pressure mass density (pm) causes outflow velocity (vo) to change, so momentum is conserved. The last equation above shows that any change in a falling mass (m) has no effect on velocity (v), so different masses fall at the same rate in a gravitational field.

Update: The above math suggests that spacetime expands at a steady rate up to light speed (c) and is slowed by the presence of matter. What about Hubble's constant and expansion velocity v = Hr?

How fast spacetime expands depends on whether you use Hubble's constant or time rate (t'). Time rate (t') grows as spacetime grows. Hubble's constant does not. The diagram below shows that spacetime can expand no more than light speed but appear to be expanding at an accelerated rate.

If we assume all the dots above are in motion, the expansion is a steady rate. If we assume that the red dot is at rest, then the blue dot appears to be moving away at light speed, and the green dot appears to be moving twice light speed! To get the right numbers for gravity, we need to go with the first assumption: spacetime expands at a steady maximum rate of light speed when it is not slowed by matter.

Update: The following equation was derived above.

The diagram below shows spacetime expanding in a gravitational field (see arrows). The net backflow or gx is c^2-v^2. As mentioned earlier, the presence of matter (a planet, star, etc.) slows the outflow rate of v.

If any mass is falling in this gravitational field, we could use these equations to describe it:

We could also use the diagrams below:

Diagram 1) above represents a small mass falling in a gravitational field. The variable u is the spacetime outflow velocity where the falling mass is located at a given moment of time. Diagram 2) represents a larger mass falling in the same field. Its corresponding outflow velocity is slower (indicated by a shorter double arrow). If we do the math for each mass, we find that the total falling velocity-squared (gx) is the same for both. This once again confirms that different masses fall at the same rate.

Update: The equations below include the dark matter effects of spacetime. As volume (V) grows, the significance of spacetime mass (psV) becomes more significant and pressure mass (increased spacetime mass caused by matter) becomes less significant. At galactic scales and beyond, most of the gravity is caused by spacetime rather than matter.

The Dark Matter and Dark Energy Effects of Spacetime

Alice and Bob don't always agree. Alice is outside our universe, looking at the big picture. She sees the universe expanding at a steady rate, like a balloon attached to a helium tank. From her point of view, what we classically think of as energy is conserved. Here's what she sees at time one (t1):

Here's what she sees at time two (t2):

Bob has a different take. He's on earth looking outward. He sees the universe expanding at an accelerated rate--the red shift of distant galaxies is greater than that of closer galaxies. Energy is not conserved--it is increasing! Here's what he sees at t1 and t2:

In the diagram above, the blue dot represents Bob's galaxy. The red dot is a galaxy far far away. As far as Bob is concerned, that red dot is moving the fastest. Bob uses equation 1) below to model what he sees; whereas, Alice uses equation 2):

Equation 1) shows velocity increasing as the radius (r) increases. However, radius (r) fails to tell us the effect gravity has on time. Where gravity is strong, time runs more slowly. Where gravity is weak, time runs faster. Gravity is weaker where the radius is larger, and vice versa. So we can substitute ct' for r in equation 1).

Alice sees the universe expanding at a steady rate. However, we can change this to ct'/t' in equation 2) to show that time (t') cancels itself. By contrast, Bob, uses Hubble's constant, a fixed time--it doesn't cancel time (t'). As a result, Alice sees a short expansion over a short time where gravity is strong, and a long expansion over a long time where gravity is weak. She sees a steady expansion velocity. Bob sees a slower velocity where gravity is strong and a faster velocity where gravity is weak.

Both Alice and Bob notice that spacetime has energy density or pressure. They both use the following equations:

Normally when there is pressure, the volume increases and that relieves the pressure. In the case of space, increasing volume just adds more energy. This keeps the pressure constant, so expansion is continuous. (Equation 5) above shows the volume (V) cancelling itself.)

Notwithstanding the added energy, Alice sees conserved energy. Using Einstein's field equations, we can derive something that shows why.

At equation 14), when the spacetime mass (ms)in the numerator increases, so does V * bar-lambda in the denominator. The increase in spacetime curvature caused by spacetime mass(energy) cancels or is always proportionate to the spacetime mass. Also, when volume (V) increases, spacetime curvature (K) decreases, so V * K is constant. The remaining variables are also constant. Thus, energy (E) is conserved.

Bob, of course, disagrees. He says the energy is growing. If we perform an operation on the conserved-energy equation, we can see why:

According to equation 17), as the universe's radius (r) increases, so does energy (E'). So who's right? Alice or Bob? Answer: they both are. What we observe depends on our frame of reference and whether we use Hubble's constant or time (t'). What Alice and Bob observed can be conveniently labeled the dark energy effects of spacetime.

Equation 15) reveals the dark matter effect. We mentioned earlier, when volume (V) grows, so does spacetime mass (ms). Variable m, however, remains constant. This means spacetime mass becomes more significant at greater volumes and matter mass becomes less significant. When we crunch the numbers, spacetime makes up most of the mass and energy within the volume of the known universe. It follows that it would cause most of the universe's gravity.

One possible mechanism for the extra gravity we observe is spacetime's expansion pressure. Imagine a weightless environment. Imagine a transparent balloon being filled with gas. Floating in the middle of that balloon is a marble. The gas pressure presses outward against the balloon's inner surface. It expands the balloon, but the pressure goes inward against the marble's surface as well.

The arrows in the above diagram represent the pressure going outward and inward. If the marble is a metaphor for a galaxy, then, in addition to gravity caused by matter, the galaxy is receiving pressure from the outside. There is also counter-pressure from within. This could give the impression of additional gravity.

Another cause of additional gravity is time (t'). Since spacetime adds more mass, the rate of time must be slower, and slower time should produce some gravitational effects.

One has to wonder, though: if the galaxies had enough gravity to attract each other, would the universe still expand? Back to the balloon. Imagine the balloon has a bunch of marbles floating inside it. They are held together by strings. Hot gas is pumped into the balloon. The balloon expands anyway. The hot gas flows around the marbles' surfaces and creates pressure on them and between them. If the strings are strong enough, the marbles won't separate. If the strings are weak, the marbles may separate and go with the flow of the hot gas in the expanding balloon. Our universe may work the same way.

Update: Here are the complete equations that model the dark matter and dark energy effects of spacetime. First we introduce some new variables:

To conserve energy we assume expanding spacetime goes in equal and opposite directions. These equal and opposite directions cancel each other. We use +/- signs to indicate that.

In the diagram above we arbitrarily label one half the spacetime volume (V) on the left as "-" and the right half as "+." Now here are the equations:

The following equation was designed to show that energy is truly conserved. No matter how big or small spacetime energy (Es) gets, overall energy is conserved. Es appears in both the numerator and denominater; it is the energy of both space and time, so it cancels itself.

Although, Bob insists that energy overall is increasing, so his equation is as follows:

Testing My Dark Matter Hypothesis

According to my hypothesis, dark matter isn't matter at all. This is why I believe Isaac Newton didn't discover it and work it into his famous equation:

Had he known that time, space or spacetime has ground-state (zero-point) energy he might have included a tiny correction term in his equation. Then again, the correction is so small it is insignificant at a local scale--hence the reason his equation works so well at such a scale. A major clue about the nature of so-called dark matter can be found in the following quote:

"When you go out to much larger distances, you encapsulate the galactic halo and a lot more dark matter."--Darin Ragozzine.

Yes, if you go out further into space you find more (cough) dark matter. This makes perfect sense if dark matter isn't matter, but spacetime. According to the theory, dark matter makes up around 85% of all matter. If this is true why the heck aren't we swimming in it? Don't you find it strange that something so plentiful should be so elusive? Here's a crude illustration of how "dark matter" comes into play:

Note the big black dot at the center, and take note of the little dots surrounding it. Let's pretend the big black dot is what we call ordinary, visible matter, and the little dots are dark matter. Within the smaller circle, the big dot accounts for most of the density. The little dots are insignificant within that region. There, Newton's equation works just fine. But when we go out further along radius (r), the little dots make up most of the density--the big dot becomes more and more insignificant.

So clearly this dark matter stuff doesn't make itself known to us at the local scale. It takes a greater region of "space" before we begin to notice its effects. To test my hypothesis, I took Einstein's field equations and did some algebra to put the variables in scalar form and to express them in terms of energy density. Why? Because energy density causes gravity (curved spacetime) and it is easier to find and plug in actual data (which is in scalar form).

At equation 4), we have the sum of two energy densities: spacetime (Ts) and visible matter (Tm). Together they make the total energy density (T). If dark matter is in fact spacetime, then we expect its energy density to be insignificant locally and more significant at large scales. Equation 5) reveals that spacetime's energy density is a very small number. Let's add it to and compare it with earth's energy density:

The above equations would make Newton very happy. Earth's energy density (ED) is huge compared to spacetime's. In fact, spacetime's ED is so insignificant, we can ignore it when determining earth's gravity. But what about the galaxy's gravity?

Ah! The tables have turned! Spacetime's energy density now causes a significant portion of the gravity. There is more than one measurement for our galaxy's energy density, depending on the method and the source. The range I found is what you see at equation 8). Taking this range into account, equation 9) shows that spacetime accounts for approximately ten percent to nearly 100% of the total ED. By contrast, "ordinary matter" constitutes approximately zero to 90% of the total ED. This confirms that spacetime has a huge impact on gravity at galactic scales. Dark matter has been under our noses all along. You can find it in any empty space.

Update: Scientists believe they have discovered a dark matter galaxy. Click here for details.

What Dark Matter Really Is

What exactly is dark matter? If you watch the above video, you will be introduced to some strange and bizarre theories involving parallel universes and higher vibrating string octaves. Ordinary matter doesn't explain the amount of gravity observed. It is assumed that galaxy clusters, and the whole universe contain far more matter than can be observed using electromagnetic signals. Such an assumption is based on the theory of General Relativity which propounds that gravity is caused by the presence of matter.

Matter and energy density curve spacetime and spacetime tells matter how to move. Gravitational acceleration (g) is currently understood and defined by the following equations (a=acceleration; t=time; x=distance; r=radius; G=Newton's constant; m=mass; gij=metric tensor; T=stress-energy tensor; v=velocity; gamma=Christoffel symbol):

It is believed that if no matter and/or energy is present, spacetime is flat and there is no gravity. Given this belief, it is not surprising that a theory of dark matter would emerge. There must be something out there responsible for all that extra gravity. But whatever it is, it does not behave like ordinary matter. In fact, it is undetectable--hence the name: dark matter.

As of this writing, no dark matter particle has been conclusively identified. I am going to go out on a limb here and make a prediction: no dark matter particle will ever be discovered. "Dark matter" is not matter at all. Something else is causing the unexplained gravity. Let me illustrate. Let's start with Einstein's field equations:

The left side contains Einstein's tensor (Gii) which is the measure of the spacetime curve. The right side contains the stress-energy tensor (Tii) which measures energy density. When energy density is zero, spacetime curvature is also zero--no gravity. Now let's turn the equation into a constant (c^4: light speed):

In the equation above, any change to the right side has no effect on the left side. Why is this important? You will see. Let's continue:

Take a close look at equation 4) above. The left side is an acceleration term. If time (t') is held constant, then no changes we make on the right side will change the acceleration term. What we have is acceleration that is independent of matter and energy. This is significant; however, we know that gravitational acceleration is not independent of matter and energy--or is it? Let's keep going. We need to define what we mean by time (t'):

Time (t') is time (t) multiplied by a Lorentz factor. We make the substitution in equation 8) above. Since both sides are acceleration terms, we can set the left side equal to gravitational acceleration (g):

According to equation 9), gravitational acceleration is not independent of changes in energy/matter (E). When E increases, so does g and when E decreases, so does g. But what happens if E is zero?

When E is zero, we still have time (t). Equation 11) above is equivalent to dark matter; albeit, it is not matter at all. We set matter to zero, so what is it? It is pure acceleration as a function of time. Gravity is not only caused by the presence of matter, it is also caused by time alone. Matter will contract time and make gravity stronger, but gravity exists even in the absence of matter. To have zero gravity requires an infinite change in time (according to equation 11). We can say with confidence that time intervals, so far, have been finite--so gravity, even in the absence of matter, is greater than zero.

Equation 11) shows that most of the gravity in our universe is caused directly by time. The remainder is indirectly caused by the relatively tiny amount of matter that make up the galaxies.