If you study physics, time and time again you will encounter various coordinate systems including Cartesian, cylindrical and spherical systems. You will also encounter the gradients and Laplacians or Laplace operators for these coordinate systems. Below is a diagram for a spherical coordinate system:
Next we have a diagram for cylindrical coordinates:
And let's not forget good old classical Cartesian coordinates:
These diagrams shall serve as references while we derive their Laplace operators. Here's what they look like:
The Cartesian Laplacian looks pretty straight forward. There's three independent variables, x, y, and z. The operator has three terms as one would expect, but check out the cylindrical operator--it has four terms and three variables. What's up with that? If you examine both the cylindrical and spherical operators, you notice terms that have factors in front of the partial derivative operators. Where do they come from and why are they necessary? To answer such questions, it pays to derive these operators from scratch.
In this post, we derive all three Laplace operators, so a side-by-side comparison can be made which further illuminates the logic behind the derivation procedure. Let's begin by expressing an arbitrary vector S in terms of each coordinate system:
The next step is to extract the unit vectors. This is done by taking partial derivatives of S with respect to each variable. For the Cartesian version, this is totally straight forward:
No normalization is required because dot products of the unit vectors give you 1's and 0's as expected:
Now, here's what we get when we take partial derivatives of the cylindrical version of S:
The unit vectors we get aren't really unit vectors. When we do dot products, we don't necessarily get 1's and 0's. Normalization is required:
Notice that one of the partial-derivative operators requires a normalization factor of 1/r. Spherical unit vectors also require normalization:
Here, two spherical partial-derivative operators require a normalization factor: 1/r and 1/rsin(theta) respectively. Now that we know the normalization factors, we can construct the gradients:
Notice how the unit vectors are placed in front of the partial-derivative operators. A common mistake is to place the unit vectors after the operators like this:
This is technically wrong or should be, since the operators are acting on the unit vectors! Here's what happens:
So we keep the unit vectors in front. This prevents errors and frustration as we perform the next step which is to square the gradients to get the Laplace operators. Let's do the easiest one first, the Cartesian gradient. We multiply each term by every other term. Doing so allows us to construct this matrix:
Here's a couple of examples of the multiplication procedure. Note that the product rule of derivatives is employed and the partial-derivative operators do in fact operate on the unit vectors, but only where it's appropriate:
The final answer is ...(drum roll) ...
Now let's square the cylindrical gradient using a similar procedure:
Looking at each term it is obvious, that once again, there is a partial-derivative operator acting on a unit vector. We can make a list of each operation we will encounter, then use the list data to make the necessary substitutions during the multiplication process.
And here's the math for the cylindrical Laplacian:
Here's the final answer:
Finally, we tackle the spherical Laplacian:
The second matrix above indicates which terms give us zero when we do the math. Below we focus on the terms that yield a value other than zero:
We gather up the terms:
Too many terms! Here's what we can do. Let's take the first couple of terms and factor out 1/r^2. Then apply the derivative product rule in reverse:
Next, take the following terms and factor out 1/{(r^2)sin(theta)}. Once again, apply the product rule in reverse:
After making substitutions, the final answer is ... (fireworks) ...



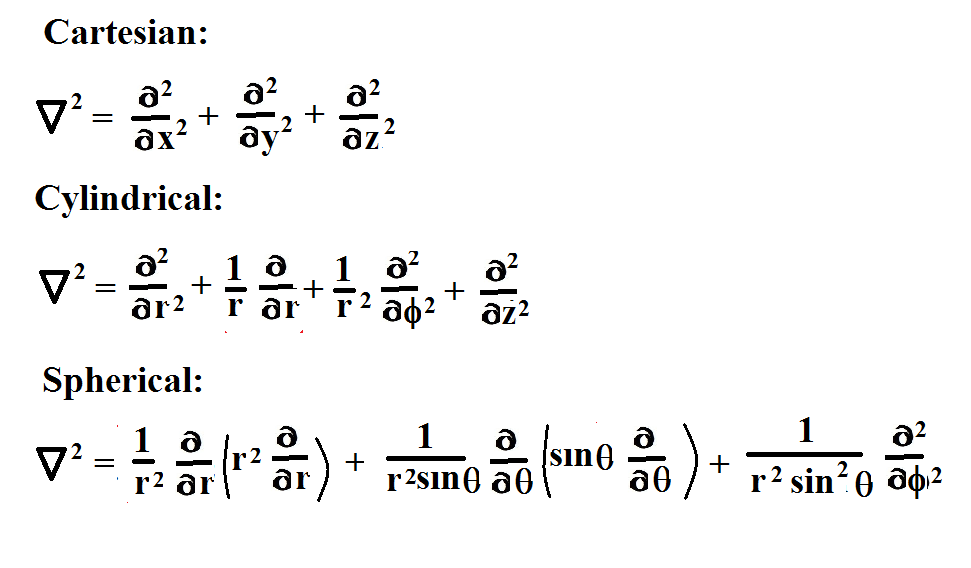



























It's really helpful.......... thankyou so much 🙏
ReplyDeleteawesome!
ReplyDeletethanks for your effort to share your knowledge for all of us who easily confused
ReplyDeleteExtremely Helpful Thanks!
ReplyDeleteThank you so much! It's really helpful.
ReplyDeleteI appreciate your effort for these derivations.